{ggdist}: How to prevent stat_dots() from overlapping stat_halfeye() in `position = "dodge&quot-CodePudding

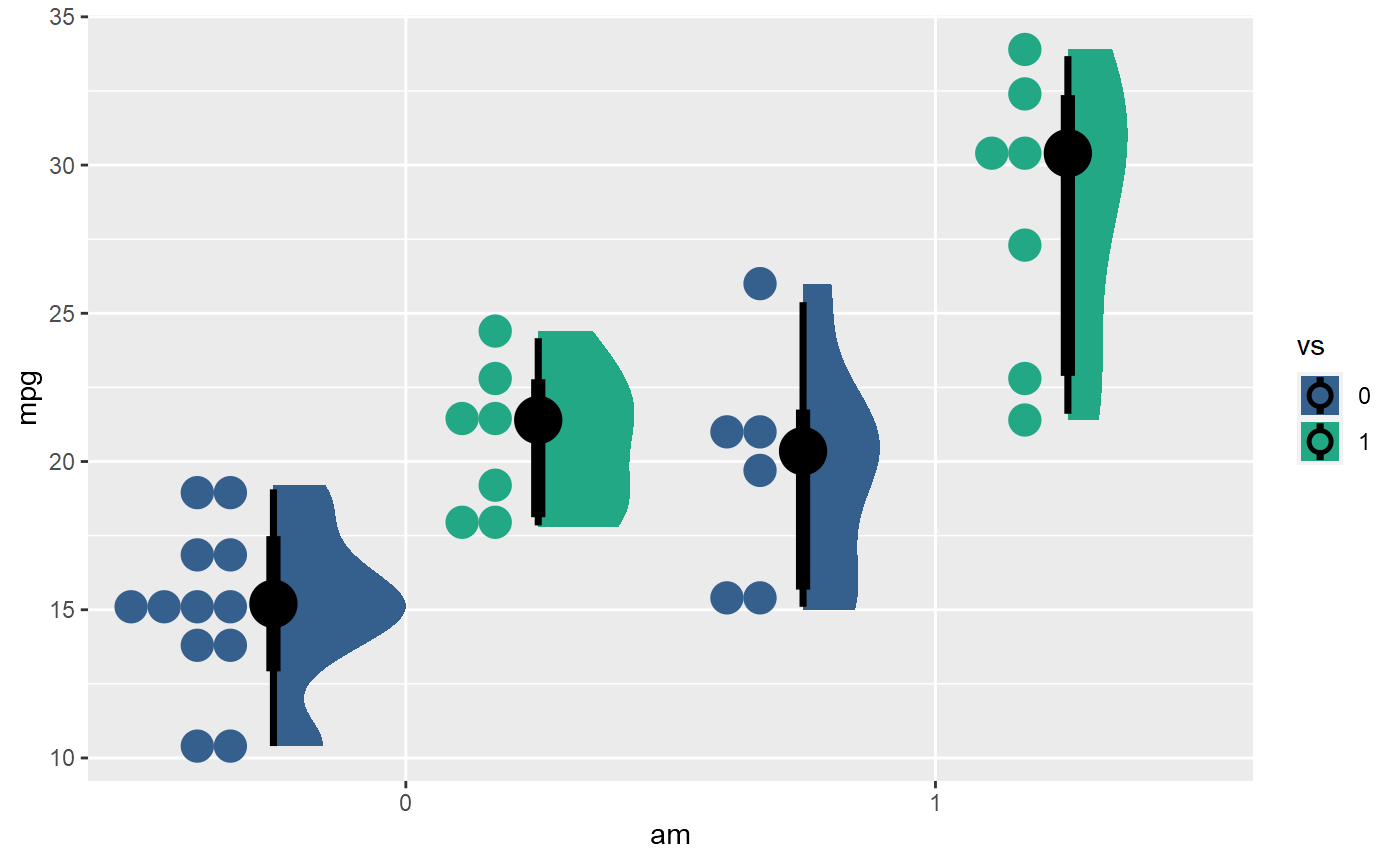
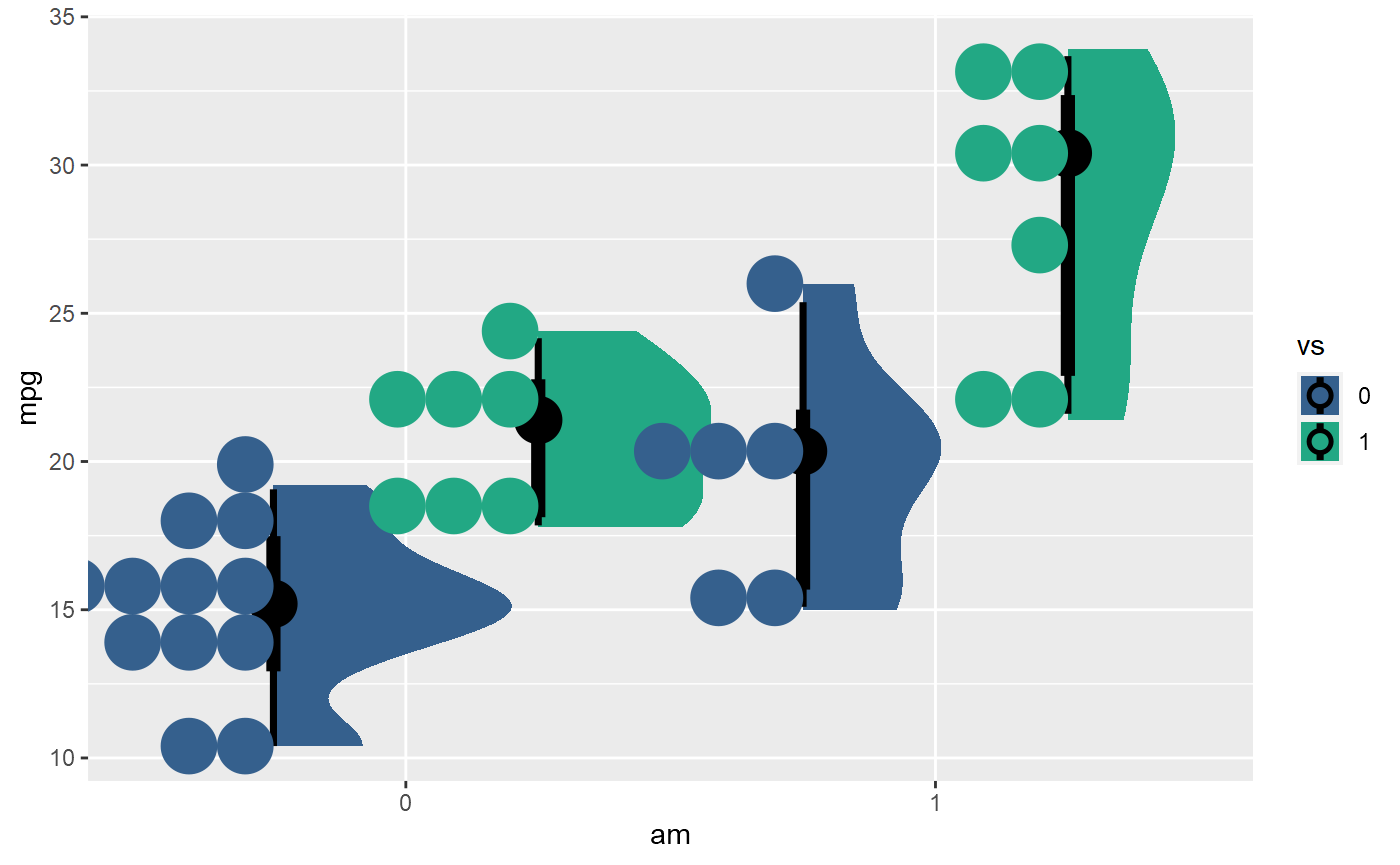
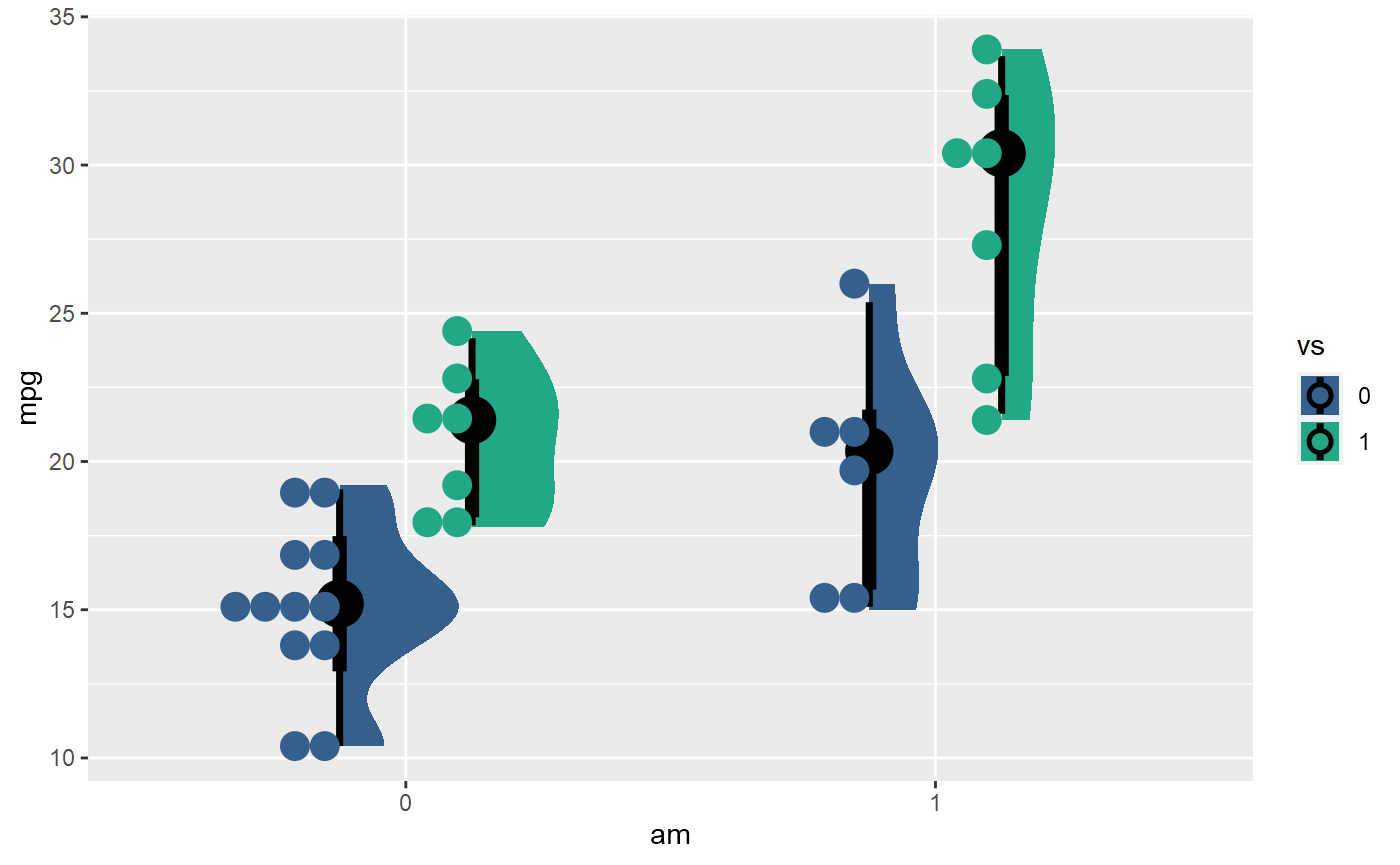
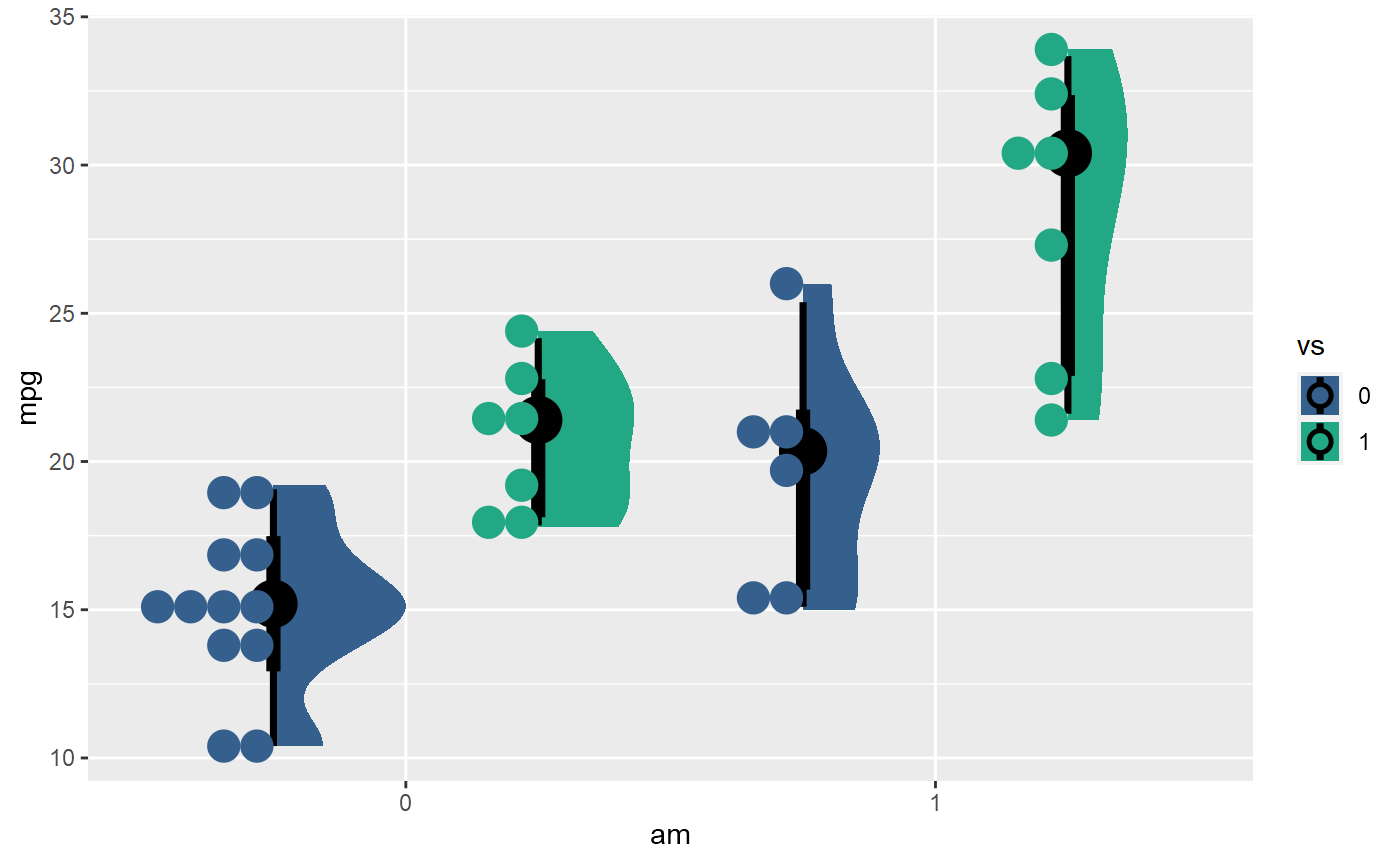
I am trying to visualise the distribution of response variable using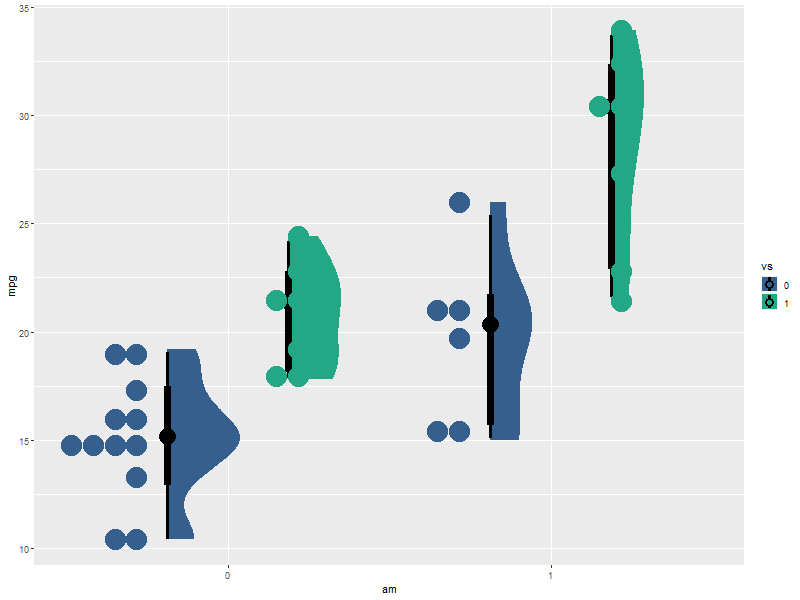

library(tidyverse)

mtcars |>
  mutate(
    am = am |>
      as.factor(),
    vs = vs |>
      as.factor()
  ) |>
  ggplot(
    aes(
      x = am,
      y = mpg,
      colour = vs,
      fill = vs
    )
  )  
  ggdist::stat_halfeye(
    # position = "dodge",
    position = position_dodge(width = 0.75),
    point_interval = median_qi,
    width = 0.5,
    .width = c(0.66, 0.95),
    interval_size_range = c(1.25, 2.5),
    interval_colour = "black",
    point_colour = "black",
    fatten_point = 3
  )  
  ggdist::stat_dots(
    position = "dodge",
    #position = "dodgejust",
    #position = position_dodge(width = 0.5),
    binwidth = 1,
    side = "left",
    dotsize = 1
  )  
  scale_fill_viridis_d(
    begin = 0.3,
    end = 0.6,
    aesthetics = c("colour", "fill")
  )

CodePudding user response：

There are three parameters you can adjust here that are relevant: position, width (equivalently height when horizontal), and scale. width/height and scale are illustrated in this diagram from the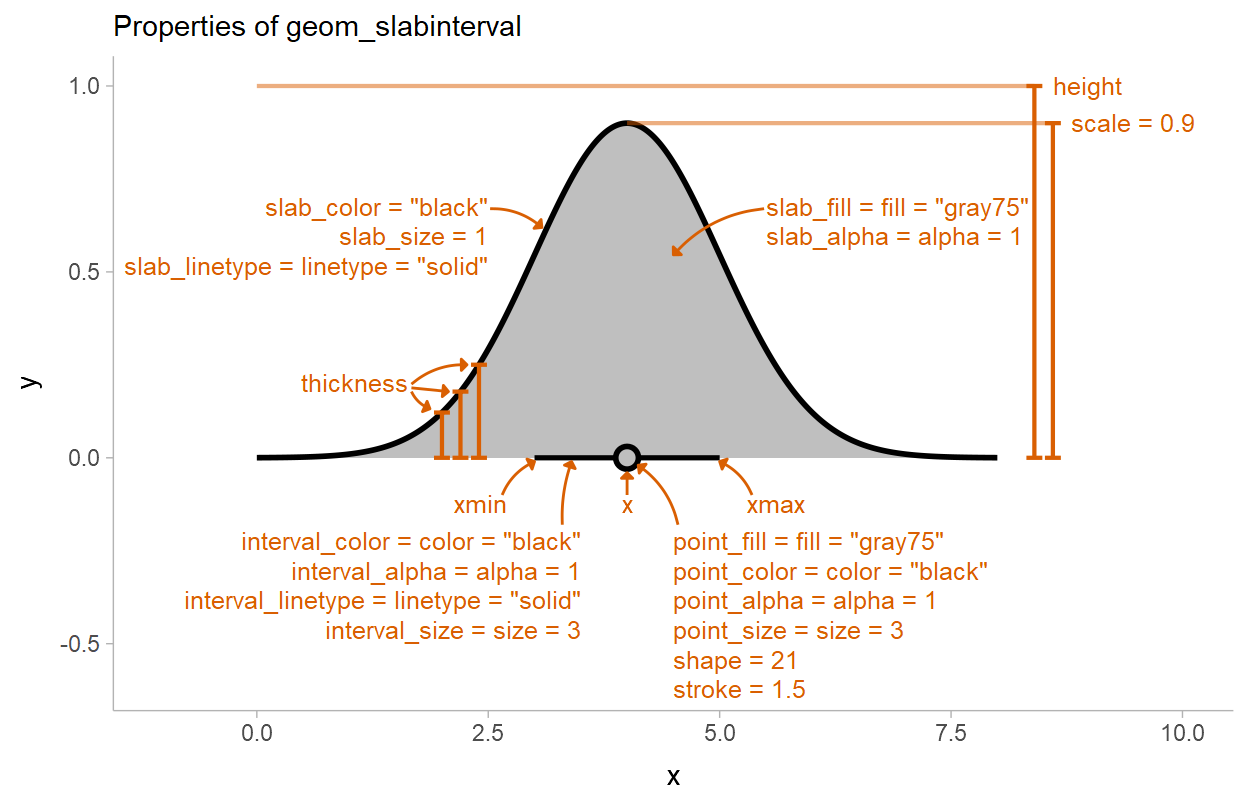

In your case, position and width can be used to adjust how the geometries are dodged and how far apart they are dodged, but I don't recommend using them to prevent overlaps. As a general rule, if you want to use two ggdist geoms together and have them dodge correctly, they should have the exact same values of position and width.

(as an aside, I just realized you are also setting binwidth manually, which is likely to make this process painful. If you use the parameters below appropriately --- particularly scale, as I will show --- it will automatically pick a binwidth to fit your dotplot into the available space. So I will omit the binwidth parameter in what follows).

If you start with this plot:

library(tidyverse)
library(ggdist)

df = mtcars |>
  mutate(
    am = am |>
      as.factor(),
    vs = vs |>
      as.factor()
  )

df |>
  ggplot(
    aes(
      x = am,
      y = mpg,
      colour = vs,
      fill = vs
    )
  )  
  ggdist::stat_halfeye(
    position = "dodge",
    point_interval = median_qi,
    .width = c(0.66, 0.95),
    interval_size_range = c(1.25, 2.5),
    interval_colour = "black",
    point_colour = "black",
    fatten_point = 3
  )  
  ggdist::stat_dots(
    position = "dodge",
    side = "left",
    dotsize = 1
  )  
  scale_fill_viridis_d(
    begin = 0.3,
    end = 0.6,
    aesthetics = c("colour", "fill")
  )

You can see the overlaps of dots and slabs. You could adjust width so that the two related subgroups within vs are closer together, but this does not guarantee no overlaps between dots and slabs, even though by chance there aren't any in this example (e.g. if the group where vs == 0 and am == 0 had some more values around 19, that density would overlap with the dots from the vs == 1 and am == 0 group):

df |>
  ggplot(
    aes(
      x = am,
      y = mpg,
      colour = vs,
      fill = vs
    )
  )  
  ggdist::stat_halfeye(
    # make sure position and width are the same for both geoms
    position = "dodge",
    width = 0.5,
    
    point_interval = median_qi,
    .width = c(0.66, 0.95),
    interval_size_range = c(1.25, 2.5),
    interval_colour = "black",
    point_colour = "black",
    fatten_point = 3
  )  
  ggdist::stat_dots(
    # position and width same as the halfeye to keep them in sync
    position = "dodge",
    width = 0.5,
    
    side = "left",
    dotsize = 1
  )  
  scale_fill_viridis_d(
    begin = 0.3,
    end = 0.6,
    aesthetics = c("colour", "fill")
  )

If you want to guarantee that the slabs and dots don't overlap, instead adjust the scale parameter. scale does not change the basic position of the geometries, instead it determines how much of the region allocated to the geometry is used to draw the slab (for geom_halfeye) or the dots (for geom_dots). When scale == 1, two adjacent slabs will just touch at their max point. Thus, if you have two geometries (like halfeye and dots) sharing the same space, you can set scale to a value less than 0.5 to guarantee they will not touch:

df |>
  ggplot(
    aes(
      x = am,
      y = mpg,
      colour = vs,
      fill = vs
    )
  )  
  ggdist::stat_halfeye(
    position = "dodge",
    scale = 0.5,
    point_interval = median_qi,
    .width = c(0.66, 0.95),
    interval_size_range = c(1.25, 2.5),
    interval_colour = "black",
    point_colour = "black",
    fatten_point = 3
  )  
  ggdist::stat_dots(
    position = "dodge",
    scale = 0.5,
    side = "left",
    dotsize = 1
  )  
  scale_fill_viridis_d(
    begin = 0.3,
    end = 0.6,
    aesthetics = c("colour", "fill")
  )

Note that while width should be the same across the two geometries, scale does not have to be. Often depending on data you can even prevent overlaps with a value greater than 0.5.

You can see further discussion and an example of rainclouds in the