foldl versus foldr for merge operator-CodePudding

Is the following statement equivalent?

foldr (  ) [ ] = foldl (  ) [ ]

I know that foldr ( ) 0 = fold ( ) 0 is equivalent and for the operator (-) it's not, but how about the ( ) operator ? I think the result is a list with the same content but in another order. Is the order of the list relevant?

CodePudding user response：

foldl :: (b -> a -> b) -> b -> [a] -> b

foldr :: (a -> b -> b) -> b -> [a] -> b

( ) is commutative, i.e. produces the same result if the arguments order is switched. E.g. 1 2 is the same as 2 1.

Look at the type signature of foldl and foldr.

foldl takes a function (b->a->b) whose second argument is an element from the list.

On the other hand, foldr takes a function (a->b->b) whose first argument is an element from the list.

With foldl, the accumulator is on the left (first argument). With foldr, the accumulator is on the right (second argument). foldl folds from left to right, foldr folds from right to left.

Technically, it's more complicated than that. For more information, see https://wiki.haskell.org/Foldr_Foldl_Foldl'

CodePudding user response：

As usual, a visual representation is better than a thousand words:

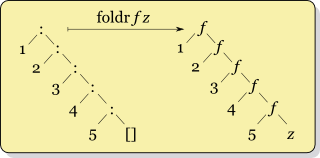
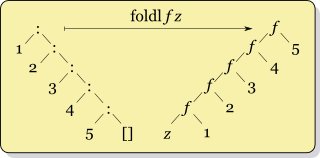
foldr foldl

(Source)

CodePudding user response：

Both expressions return the in order concatenation of all sublists in the rightmost argument, so they are functionally identical, at least for finite sublists.

Let's check using the Haskell ghci interpreter:

$ ghci
GHCi, version 8.10.5: https://www.haskell.org/ghc/  :? for help
 ...
 λ> 
 λ> 
 λ> foldr (  ) [] [[1,2],[3,4,5],[6,7,8,9]] == foldl (  ) []    [[1,2],[3,4,5],[6,7,8,9]]
 True
 λ> 
 λ> foldr (  ) [] [[1,2],[3,4,5],[6,7,8,9]]
 [1,2,3,4,5,6,7,8,9]
 λ> 
 λ> foldl (  ) [] [[1,2],[3,4,5],[6,7,8,9]]
 [1,2,3,4,5,6,7,8,9]
 λ>

But that's not the whole story. For example, any programmer who has been thru the usual lectures about sorting algorithms knows that bubble sort and QuickSort are functionally equivalent. Both algorithms return the ordered version of the input list.

But QuickSort is practical, and bubble sort is useless except for very short lists.

It is a bit similar here.

Let's turn statistics on in our ghci interpreter:

 λ> 
 λ> :set  s
 λ> 
 λ> length $ foldl (  ) [] (replicate 5000 [1,2,3,4])
 20000
 (3.31 secs, 4,124,759,752 bytes)
 λ> 
 λ> length $ foldl (  ) [] (replicate 10000 [1,2,3,4])
 40000
 (16.94 secs, 17,172,001,352 bytes)
 λ>

So if we double the number of input sublists, the volume of memory allocations is multiplied by 4, not 2. The algorithm is quadratic here, hence horribly slow, like bubble sort.

And no, replacing foldl by its strict sibling foldl' will not help. The root of the problem is that operator ( ) has to duplicate its left operand, because it is not feasible in Haskell to just alter its last pointer to next node, like you would do in C/C . However, operator ( ) can just use a simple pointer to its right operand, because the right operand is immutable, as is any Haskell named value.

In summary, for the left operand, immutability works against us. For the right operand, it works for us. This is what breaks the performance symmetry between foldl and foldr.

We can readily check that the performance of foldr is much better:

 λ> 
 λ> length $ foldr (  ) [] (replicate 5000 [1,2,3,4])
 20000
 (0.02 secs, 1,622,304 bytes)
 λ> 
 λ> length $ foldr (  ) [] (replicate 10000 [1,2,3,4])
 40000
 (0.02 secs, 3,182,304 bytes)
 λ>

because memory allocation here is multiplied by 2, not 4.