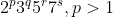Looking within the xcorr function, most of it is pretty straightforward, except for one function within xcorr called "findTransformLength".

function m = findTransformLength(m)
    m = 2*m;
    while true
        r = m;
        for p = [2 3 5 7]
            while (r > 1) && (mod(r, p) == 0)
                r = r / p;
            end
        end
        if r == 1
            break;
        end
        m = m   1;
    end

With no comments, i fail to understand what this function is meant to acheive and what is the significance of p = [2 3 5 7]. Why those numbers specifically? Why not take a fixed FFT size instead? Is there a disadvantage(cause errors) to taking a fixed FFT size?

CodePudding user response：

This part is used to get the integer closest to 2*m that can be written in the form:

Either:

1. m is already of this form, then the loop

   for p = [2 3 5 7]
            while (r > 1) && (mod(r, p) == 0)
                r = r / p;
            end
    end
   

Will decrease r down to 1 and the break will be reached.

2. Or m has at least one other prime factor, and r will not reach 1. You go back to the look with m 1 and so on until you reach a number of the right form.

As per why they do this, you can see on the fft doc, in the Input arguments section:

n — Transform length [] (default) | nonnegative integer scalar

Transform length, specified as [] or a nonnegative integer scalar. Specifying a positive integer scalar for the transform length can increase the performance of fft. The length is typically specified as a power of 2 or a value that can be factored into a product of small prime numbers. If n is less than the length of the signal, then fft ignores the remaining signal values past the nth entry and returns the truncated result. If n is 0, then fft returns an empty matrix.

Example: n = 2^nextpow2(size(X,1))