How to calculate the positions of new points after rotating the image around arbitrary axis-CodePudding

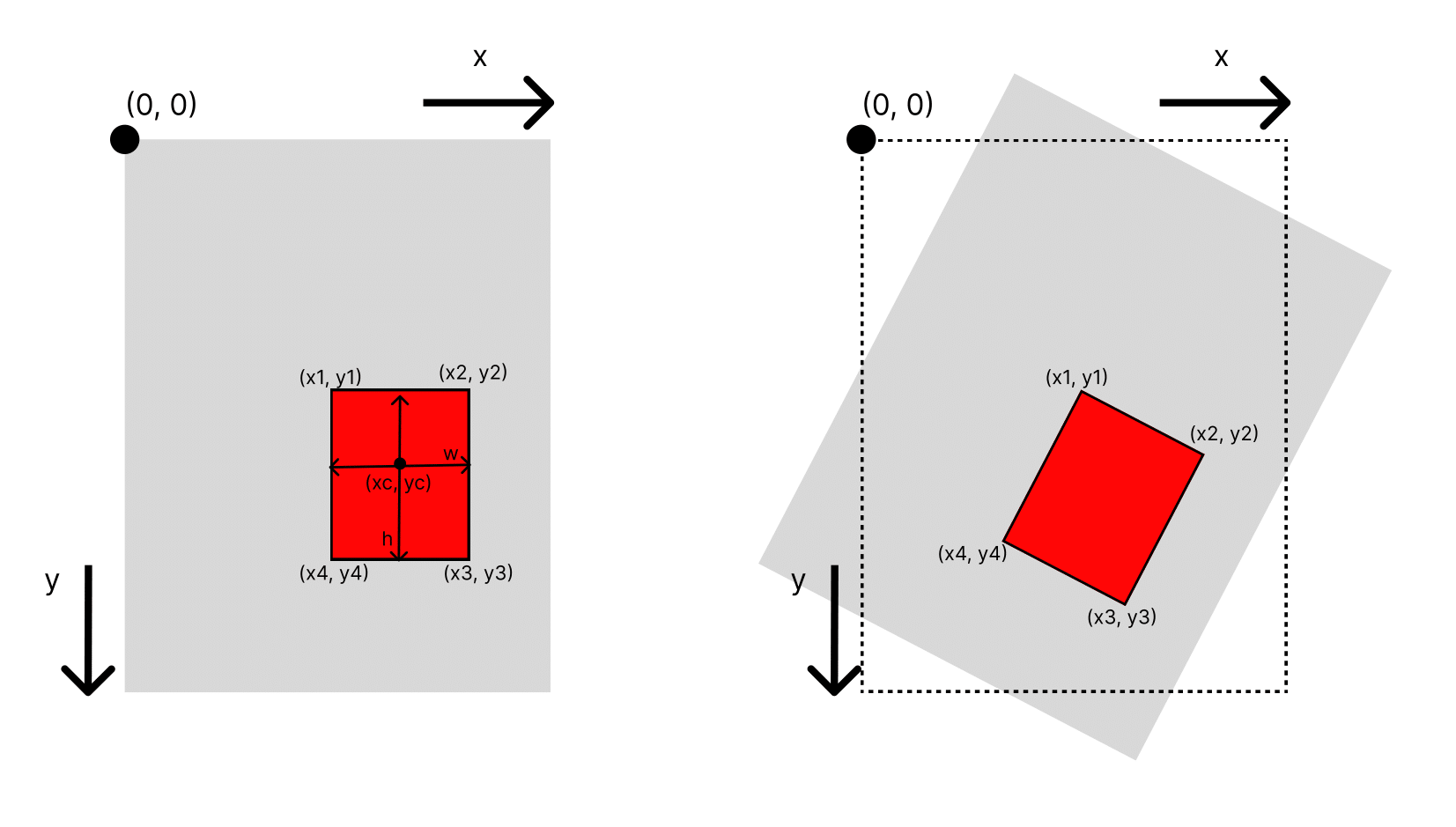
Having a dataset of aligned objects, I would like to augment it by applying random rotations with the axis at the center of the object. Below is the rotation representation (left original, right image rotated around the point (xc, yc). for rotation, I have used the following logic:

import cv2
import random
image_source = cv2.imread('sample.png')
height, width = image_source.shape[:2]
random_angle = random.uniform(90, 90)
yolo_annotation_sample = get_annotation() # this function retrieves yolo annotation
label_id, xc, yc, object_width, object_height = yolo_annotation_sample # e.g. 4, 0.0189, 0.25, 0.0146, 0.00146

center_x = width * xc
center_y = height * yc
left = center_x - (width * object_width) / 2
top = center_y - (height * object_height) / 2
right = left   width * object_width
bottom = top   height * object_height

M = cv2.getRotationMatrix2D((cx, cy), random_angle, 1.0)
image_rotated = cv2.warpAffine(image_source, M, (width, height))
# logic for calculating new point position (doesn't work)
x1_y1 = np.asarray([[left, top]]) 
x1_y1_new = np.dot(x1_y1, M)
x2_y2 = np.asarray([[right, top]]) 
x2_y2_new = np.dot(x2_y2, M)
x3_y3 = np.asarray([[right, bottom]]) 
x3_y3_new = np.dot(x3_y3, M)
x4_y4 = np.asarray([[left, bottom]]) 
x4_y4_new = np.dot(x4_y4, M)

Does anyone know how to recalculate the point(s) after rotating around the arbitrary point as shown above?

CodePudding user response：

Use cv2.transform(points, M). Points with shape: (4, 1, 2). Full code:

import cv2
import random
import numpy as np

image_source = cv2.imread('sample.png')
height, width = image_source.shape[:2]
random_angle = 40 #random.uniform(90, 90)
yolo_annotation_sample = (4, 0.6189, 0.25, 0.246, 0.0846) # this function retrieves yolo annotation
label_id, xc, yc, object_width, object_height = yolo_annotation_sample

center_x = width * xc
center_y = height * yc
left = center_x - (width * object_width) / 2
top = center_y - (height * object_height) / 2
right = left   width * object_width
bottom = top   height * object_height

cx, cy = width / 2, height / 2
M = cv2.getRotationMatrix2D((cx, cy), random_angle, 1.0)
image_rotated = cv2.warpAffine(image_source, M, (width, height))
# logic for calculating new point position (doesn't work)
bbox_points = [[left, top], [right, top], [right, bottom], [left, bottom]]
bbox_points = np.array(bbox_points).reshape((-1,1,2))
rotated_points = cv2.transform(bbox_points, M) # what you need

cv2.polylines(image_source,[bbox_points.astype(int)],True,(255,100,0), 10)
cv2.polylines(image_rotated,[rotated_points.astype(int)],True,(255,100,0), 10)

cv2.imshow("orig", image_source)
cv2.imshow("rotated", image_rotated)
cv2.waitKey()

CodePudding user response：

Look at [https://en.wikipedia.org/wiki/Transformation_matrix][1]

Once I tried to calculate it myself:

class rotm :
 '''set up rotation matrix'''
 def __init__(self,axis,angle,unit="radians") :   
  self.m = scipy.zeros((4,4),scipy.float128)
  if unit=="radians" :
   angler = angle
  else :
   angler = math.radians(angle)
  pass
  if axis=='x' :
   self.m[0][0]=1.0
   self.m[1][1]=math.cos(angler)
   self.m[2][2]=self.m[1][1]
   self.m[3][3]=1.0
   self.m[1][2]=-math.sin(angler)
   self.m[2][1]=-self.m[1][2]
  elif axis=='y' :
   self.m[0][0]=math.cos(angler)
   self.m[1][1]=1.0
   self.m[2][2]=self.m[0][0]
   self.m[3][3]=1.0
   self.m[0][2]=math.sin(angler)
   self.m[2][0]=-self.m[0][2]
  elif axis=='z' :
   self.m[0][0]=math.cos(angler)
   self.m[1][1]=self.m[0][0]
   self.m[2][2]=1.0
   self.m[3][3]=1.0
   self.m[0][1]=-math.sin(angler)
   self.m[1][0]=-self.m[0][1]
  pass         
 pass
 def fPrint(self) :
  '''auxiliary function: print transformation matrix '''      
  print(self.m)   
 pass     
pass #end of rotm class