How to get all combination between N objects with K values C#-CodePudding

I'm looking for an algorithm that can solve my issue. I'm working on a project which deals with products and their attributes. Here I have a product that has N number of options and the options each have K number of values. For example, a Laptop has color, memory, and display options. Each of these has different values. What I need is to create multiple product variations from this single product. This means I need a variation for each possible combination between the options I have. See the image for a better explanation. I'm working with C#. 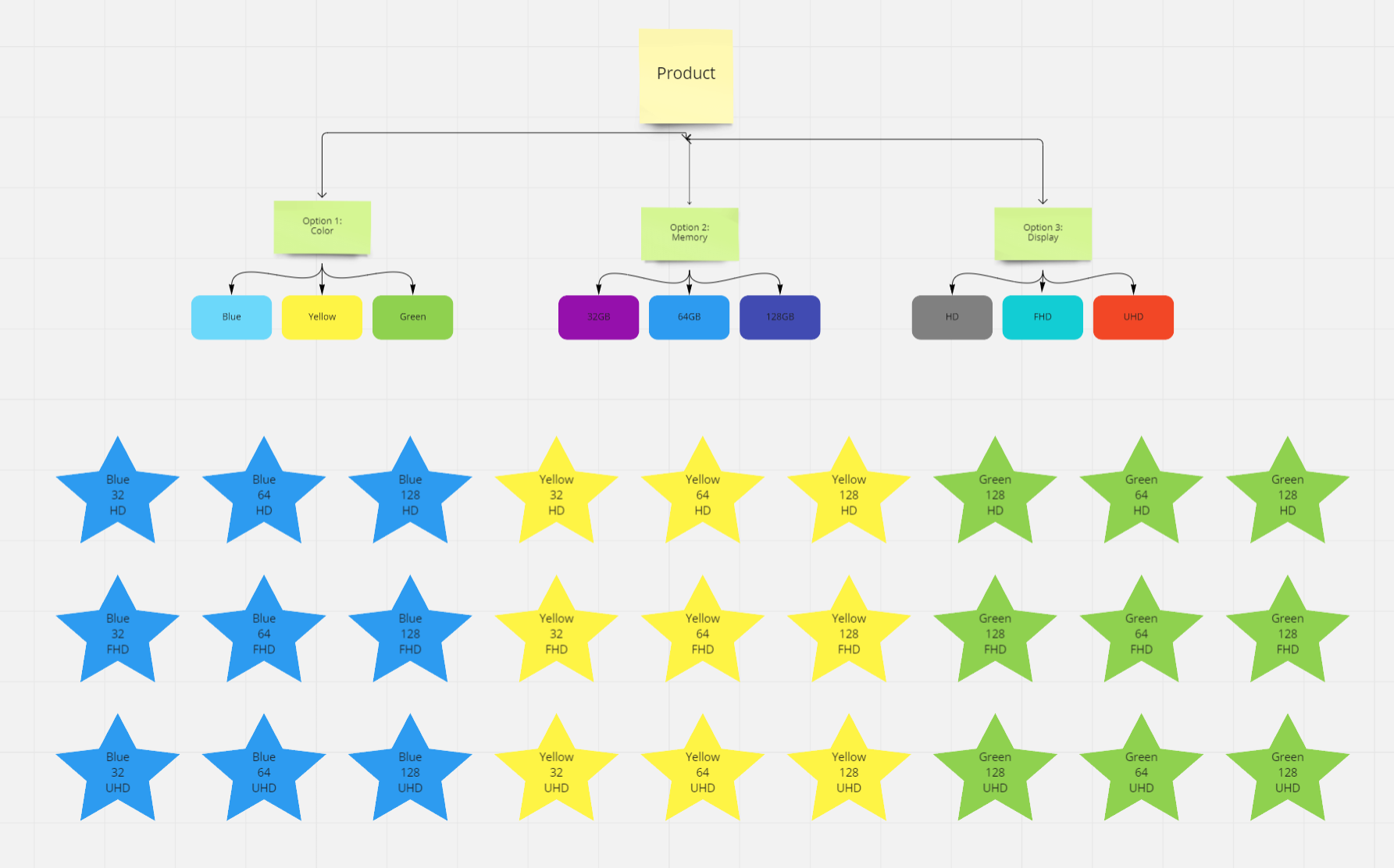Diagram of all product variations

Keep in mind that this needs to be dynamic, as for each product I may have different amounts of oprion and different amount of otion values.

Thanks for your answers.

CodePudding user response：

Simple idea:

    string[] colors = { "red", "green", "blue"};    //option 1 
    int[] mem = { 32, 64, 128 };                    //option 2
    string[] display = {"HD", "FHD", "UHD" };       //option 3
    
    foreach (var color in colors)
    {
        foreach (var size in mem)
        {
            foreach(var resolution in display)
            {
                Console.WriteLine(color   " "   size.ToString()   " "   resolution);
            }
        }
    }

Or you can do it with List

List<string> colors = new List<string>();
colors.Add("gray");
colors.Add("transparent");

CodePudding user response：

Based on my understanding of your description, I would say that a product may be represented by the following class:

public class Product
{
    public List<Option> Options { get; set; }
    
    public List<List<string>> GetAllCombinations()
    {
        // TODO
    }
}

public class Option
{
    public string Name { get; set; }
    
    public List<string> Values { get; set; }
}

Your question is then:

What needs to happen inside GetAllCombinations() to give you the expected result?

What size of N and K are we talking about? If they do not get much larger than in your example scenario, the following implementation is a possible approach:

public List<List<string>> GetAllCombinations()
{
    if (Options == null || !Options.Any())
    {
        return new();
    }
    
    var combinations = new List<List<string>> { new() };
    
    foreach (var option in Options)
    {
        combinations = combinations
            .SelectMany(combination => option.Values
                .Select(optionValue => new List<string>(combination) { optionValue }))
            .ToList();
    }
    
    return combinations;
}

What happens inside the .SelectMany() is basically:

For each existing combination, create one new combination per option value that consists of the existing combination and the option value.

Notice that combinations is created as a list containing an empty list. Starting off with an empty list inside the outer list (rather than the outer list being empty) is key here, seeing as each new combination set is always created based on the existing content of combinations; i.e. if combinations is an empty list to begin with, it will simply never be populated.

The population of combinations is perhaps easier to visualize with a detailed example. Let us create a product similar to the one you have described in your question post and generate all combinations as follows:

Product product = new()
{
    Options = new()
    {
        new() { Name = "Color", Values = new() { "Blue", "Yellow", "Green" } },
        new() { Name = "Memory", Values = new() { " 32 GB", " 64 GB", "128 GB" } },
        new() { Name = "Display", Values = new() { " HD", "FHD", "UHD" } },
    }
};

var combinations = product.GetAllCombinations();

The content of combinations inside GetAllCombinations() will be the following:

combinations after creation:

{
    { } // empty list
}

combinations after first iteration of the foreach loop:

{
    { "Blue"   },
    { "Yellow" },
    { "Green"  }
}

combinations after second iteration of the foreach loop:

{
    { "Blue",      " 32 GB" },
    { "Blue",      " 64 GB" },
    { "Blue",      "128 GB" },
    { "Yellow",    " 32 GB" },
    { "Yellow",    " 64 GB" },
    { "Yellow",    "128 GB" },
    { "Green",     " 32 GB" },
    { "Green",     " 64 GB" },
    { "Green",     "128 GB" },
}

combinations after third (last) iteration of the foreach loop:

{
    { "Blue",      " 32 GB",    " HD" },
    { "Blue",      " 32 GB",    "FHD" },
    { "Blue",      " 32 GB",    "UHD" },
    { "Blue",      " 64 GB",    " HD" },
    { "Blue",      " 64 GB",    "FHD" },
    { "Blue",      " 64 GB",    "UHD" },
    { "Blue",      "128 GB",    " HD" },
    { "Blue",      "128 GB",    "FHD" },
    { "Blue",      "128 GB",    "UHD" },
    { "Yellow",    " 32 GB",    " HD" },
    { "Yellow",    " 32 GB",    "FHD" },
    { "Yellow",    " 32 GB",    "UHD" },
    { "Yellow",    " 64 GB",    " HD" },
    { "Yellow",    " 64 GB",    "FHD" },
    { "Yellow",    " 64 GB",    "UHD" },
    { "Yellow",    "128 GB",    " HD" },
    { "Yellow",    "128 GB",    "FHD" },
    { "Yellow",    "128 GB",    "UHD" },
    { "Green",     " 32 GB",    " HD" },
    { "Green",     " 32 GB",    "FHD" },
    { "Green",     " 32 GB",    "UHD" },
    { "Green",     " 64 GB",    " HD" },
    { "Green",     " 64 GB",    "FHD" },
    { "Green",     " 64 GB",    "UHD" },
    { "Green",     "128 GB",    " HD" },
    { "Green",     "128 GB",    "FHD" },
    { "Green",     "128 GB",    "UHD" }
}

Example fiddle here.