Dijkstra's algorithm with secondary cost limitation-CodePudding

As part of a school assignment, I am required to implement Dijkstra's algorithm on a weighted, cyclic graph with a caveat - there exist a secondary weight/cost (henceforth referred to as B) on each edge, and the algorithm is to find the shortest path from a source node to a target node while keeping total B to be under a certain constant value.

On top of basic Dijkstra's, I have added an additional condition to the relaxation/update condition, which is that the current shortest path must be under the constant B value given.

if (no shortest path yet exists to neighbour node X or the current shortest path to the neighbour node is longer than the current shortest path to current node   current edge to neighbour node) and total **B** of current shortest path to current node   current edge to neighbour node is less than input **B** value:

   update current shortest path to neighbour node

However, the result returned, is neither the shortest path or has the lowest B. In other words, there exists other paths with lower distance as well as cost B. May I ask what is the problem with my understanding?

Edit: Current Code:

class Node:
    def __init__(self, node, p): 
        self.node = node
        self.p = p

    def __lt__(self, other):
        return self.p < other.p
    

def b_dijkstra(G, S, T, constraint):
    start = [Node(S, 0.0)]                       # Creating initial start node using HeapQ and setting its value to 0.0
    goal = set()
    pred = dict()                                                         # Dictionary to store visited nodes in a graph
    dist = dict()                                                     # Dictionary to store distance from point to point
    b = dict()
    pred[S] = None
    dist[S] = 0.0
    b[S] = 0.0
    count = 0
    while start:
        count  = 1
        C = hq.heappop(start).node                   # Pop the smallest item off the heap, maintaining the heap invariant.
        if C == T:
            print('Nodes searched:',count)
            print(' b:', b[C])
            return traversal(T, pred)
        goal.add(C)
        #for each neighbour
        for pointer in G[C]:
            if pointer in goal:
                continue
            dist_temp = dist[C]   G[C][pointer]['weight']
            b_temp =  b[C]   G[C][pointer]['b']
            if (pointer not in dist or dist[pointer] > dist_temp) and constraint >= b_temp: #if stored distance is greater than the calculated distance
                dist[pointer] = dist_temp
                pred[pointer] = C
                b[pointer] =  b_temp
                hq.heappush(start, Node(pointer, dist[C]   G[C][pointer]['weight']))          # Adding vertex to queue
    return []

CodePudding user response：

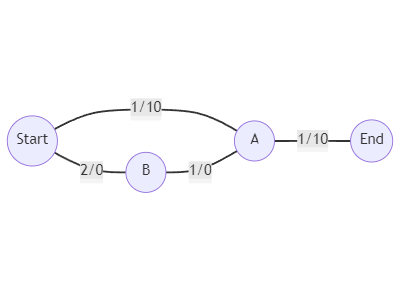
Let's assume you have this graph (weights given as weight/B) with a limit on B of 15. What will your algorithm do? If I understand you correctly, it will first find the shortest path to A costing 1/10 and then fail to find any path to End satisfying the condition on B. Is my understanding correct? If yes, it should be clear what is wrong with your algorithm.