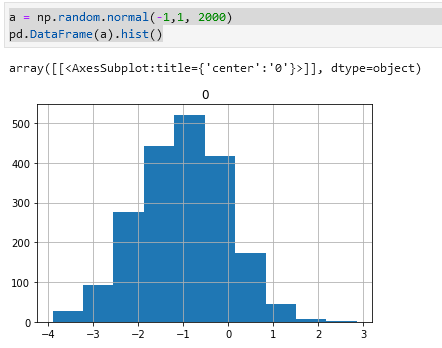
I am developing a shallow fully connected ANN from scratch which learns thanks to the Gradient Descent with momentum algorithm. This is the code
import numpy as np
from scipy.special import expit, xlog1py
def softmax(y):
e_y = np.exp(y - np.max(y))
return e_y / e_y.sum()
def cross_entropy(y, t, derivative=False, post_process=True):
if post_process:
if derivative:
return y - t
return -np.sum(np.sum(xlog1py(t, softmax(y)), axis=0))
def sigmoid(a, derivative=False):
f_a = expit(-a)
df_a = np.multiply(f_a, (1 - f_a)) # element-wise
if derivative:
return df_a
return f_a
def identity(a, derivative=False):
f_a = a
df_a = np.ones(np.shape(a))
if derivative:
return df_a
return f_a
def generate_data(n_items, n_features, n_classes):
X = np.asmatrix(np.random.normal(size=(n_items, n_features)))
targets = np.asarray(np.random.randint(n_classes, size=n_items))
targets = one_hot(targets)
return X, targets
def one_hot(targets):
return np.asmatrix(np.eye(np.max(targets) 1)[targets]).T
class NeuralNetwork:
def __init__(self):
self.layers = []
def add_layer(self, layer):
self.layers.append(layer)
def build(self):
for i, layer in enumerate(self.layers):
if i == 0:
layer.type = "input"
else:
layer.type = "output" if i == len(self.layers) - 1 else "hidden"
layer.configure(self.layers[i - 1].neurons)
def fit(self, X, targets):
MAX_EPOCHS = 200
epoch_loss = []
# batch mode
for epoch in range(MAX_EPOCHS):
predictions = self.predict(X)
self.back_prop(targets, cross_entropy)
self.learning_rule(l_rate=0.01, momentum=0.01)
loss = cross_entropy(predictions, targets)
epoch_loss.append(loss)
print("E(%d) on TrS is:" % epoch, loss)
# Columns of predictions
def predict(self, dataset):
z = dataset.T
for layer in self.layers:
z = layer.forward_prop_step(z)
return z
def back_prop(self, target, loss):
for i, layer in enumerate(self.layers[:0:-1]):
next_layer = self.layers[-i]
prev_layer = self.layers[-i - 2]
layer.back_prop_step(next_layer, prev_layer, target, loss)
def learning_rule(self, l_rate, momentum):
# Momentum GD
for layer in [layer for layer in self.layers if layer.type != "input"]:
layer.update_weights(l_rate, momentum)
layer.update_bias(l_rate, momentum)
class Layer:
def __init__(self, neurons, type=None, activation=None):
self.dE_dW = 0
self.dE_db = 0
self.dEn_db = None
self.dEn_dW = None
self.dact_a = None
self.out = None
self.weights = None
self.bias = None
self.w_sum = None
self.neurons = neurons
self.type = type
self.activation = activation
self.deltas = None
def configure(self, prev_layer_neurons):
self.weights = np.asmatrix(np.random.normal(-1, 1, (self.neurons, prev_layer_neurons)))
self.bias = np.asmatrix(np.random.normal(-1, 1, self.neurons)).T # vettore colonna
if self.activation is None:
# th approx universale
if self.type == "hidden":
self.activation = sigmoid
elif self.type == "output":
self.activation = identity
def forward_prop_step(self, z):
if self.type == "input":
self.out = z
else:
self.w_sum = np.dot(self.weights, z) self.bias
self.out = self.activation(self.w_sum)
return self.out
def back_prop_step(self, next_layer, prev_layer, target, local_loss):
if self.type == "output":
self.dact_a = self.activation(self.w_sum, derivative=True)
self.deltas = np.multiply(self.dact_a,
local_loss(self.out, target, derivative=True)) # (c,batch_size)
else:
self.dact_a = self.activation(self.w_sum, derivative=True) # (m,batch_size)
debug = np.dot(next_layer.weights.T, next_layer.deltas) # <<<< problem here
self.deltas = np.multiply(self.dact_a, debug)
self.dEn_dW = self.deltas * prev_layer.out.T
self.dEn_db = self.deltas
self.dE_dW = self.dEn_dW
self.dE_db = self.dEn_db
def update_weights(self, l_rate, momentum):
# Momentum GD
self.weights = self.weights - l_rate * self.dE_dW
self.weights = -l_rate * self.dE_dW momentum * self.weights
def update_bias(self, l_rate, momentum):
# Momentum GD
self.bias = self.bias - l_rate * self.dE_db
self.bias = -l_rate * self.dE_db momentum * self.bias
if __name__ == '__main__':
# Dog: 0 -> 000
# Cat: 1 -> 010
# Mouse: 2 -> 001
net = NeuralNetwork()
d = 4 # (n_features)
c = 3 # classes
n_items = 10 # increasing this gives NaN in EBP formula, in debug variable
for m in (d, 4, c):
layer = Layer(m)
net.add_layer(layer)
net.build()
X, targets = generate_data(n_items=n_items, n_features=d, n_classes=c)
net.fit(X, targets)
If n_items value is low, such as 10 or 100, the learning works properly:
E(0) on TrS is: -0.27547576455869305
E(1) on TrS is: -0.33774479466660445
E(2) on TrS is: -0.3295771015279694
...
E(199) on TrS is: -0.33026951829371987
Unfortunately when n_items gets bigger, such as 1000 I get this error:
RuntimeWarning: invalid value encountered in multiply self.deltas = np.multiply(self.dact_a, debug)
and:
E(0) on TrS is: -0.3337489007828587
E(1) on TrS is: -0.01614463421285259
E(2) on TrS is: -0.33594156066981384
E(3) on TrS is: -0.11378512597000995
E(4) on TrS is: -0.33508867936192843
E(5) on TrS is: -0.33276323614435077
E(6) on TrS is: -0.33310949105565746
E(7) on TrS is: -0.224661060748479
E(8) on TrS is: -0.3321560115270673
E(9) on TrS is: -0.22289014654421438
...
E(138) on TrS is: nan
E(139) on TrS is: nan
E(140) on TrS is: nan
E(141) on TrS is: nan
...
E(199) on TrS is: nan
I think this is caused by debug variable which grows until it reaches the sys.float_info.max value which is 1.7976931348623157e 308.
How can I solve this problem?
CodePudding user response:
It looks like you have exploding gradients. Maybe try some regularisation.
A couple of general things though. Your weight initialisation is going to give very large starting values which can lead to exploding gradients in itself.
Instead, consider something more like:
np.random.normal(-0.1,0.02,...
This example doesn't affect the weights, but it is also worth looking at the logic of some of your methods. For instance, sigmoid always calculates the derivative whether it is used or not. Perhaps instead use two methods (one job per method) or at least calculate the derivative inside the if:
def sigmoid(a, derivative=False):
f_a = expit(-a)
if derivative:
df_a = np.multiply(f_a, (1 - f_a)) # element-wise
return df_a
return f_a
For more about exploding gradients and weights initialisation, see this https://medium.com/usf-msds/deep-learning-best-practices-1-weight-initialization-14e5c0295b94 .