I'm trying to calculate pi with the precision of 10 decimal places. And the efficiency has to be the best(speed and memory allocation). The programming language is C in CodeBlocks.

I don't want to change the formula I'm using: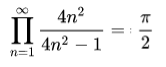

Problem: after a while, the resulting number stops incrementing but the iteration doesn't stop.

I'm not sure if this is a math problem or some kind of variable overflow.

The resulting number is 3.1415926431 and the number I want to achieve is 3.1415926535. Every time the incrementation stops at this specific number and the iteration continues. Is there a possibility of an overflow or something?

Now I'm printing out every thousandth iteration (just the see the process) This will be deleted in the end.

notice the a = n; a *= 4 * a; is for memory efficiency, there are more similar cuts I did.

code I'm using

#include <stdio.h>
#include <math.h>
#include <time.h>

int main(){
    double time_spent = 0.0;
    clock_t begin = clock();
    int n=1;
    double resultNumber= 1;
    double pi = 3.1415926535;
    double pi2 = pi / 2;
    double a;
    while(1){
        a = n;
        a *= 4 * a;
        resultNumber *= a / (a - 1);
        n  ;

        if (fabs(resultNumber - pi2) < pow(10,-10))
            break;

        if (n00==0) {
            printf("%.10f %d\n", resultNumber*2, n);
        }
    }

    clock_t end = clock();
    time_spent  = (double)(end - begin) / CLOCKS_PER_SEC;
    printf("The elapsed time is %f seconds", time_spent);
    return 0;
}

You can try it out here: https://onlinegdb.com/q2Gil1DHdy

CodePudding user response：

Is there a possibility of an overflow or something?

The precision of floating-point numbers is limited. In a typical C implementation, double has 53 bits of mantissa, which corresponds to about 15 significant decimal digits. But the range of such FP numbers is much larger than /- 10¹⁵, so when your FP number is large enough, the units digit is not significant. Then subtracting 1 from it will not produce a different number. When your a reaches that point, the quotient a / (a - 1) will be identically 1, so multiplying by that will not change the working result.

It's possible that you would get enough additional precision by using long double instead of double. That might help both in getting you more terms in your product before the problem described above sets in, and also by reducing the relative magnitude of FP rounding errors earlier in the computation.

CodePudding user response：

You can rescue a little of the accuracy by the following trick:

4n² / (4n² - 1) = 1   1 / (4n² - 1)

For large n, these factors are close to 1 and challenge the floating-point representation. You can use the identity

(1   a)(1   b)(1   c)... = 1   (a   b   c...)   (ab   ac   ...   bc   ...) ...

So for small terms a, b, c... (when the second order terms disappear), it is more accurate to use the approximation 1 (a b c...), of course summing inside the parenthesis first.