I'm working on the Leetcode problem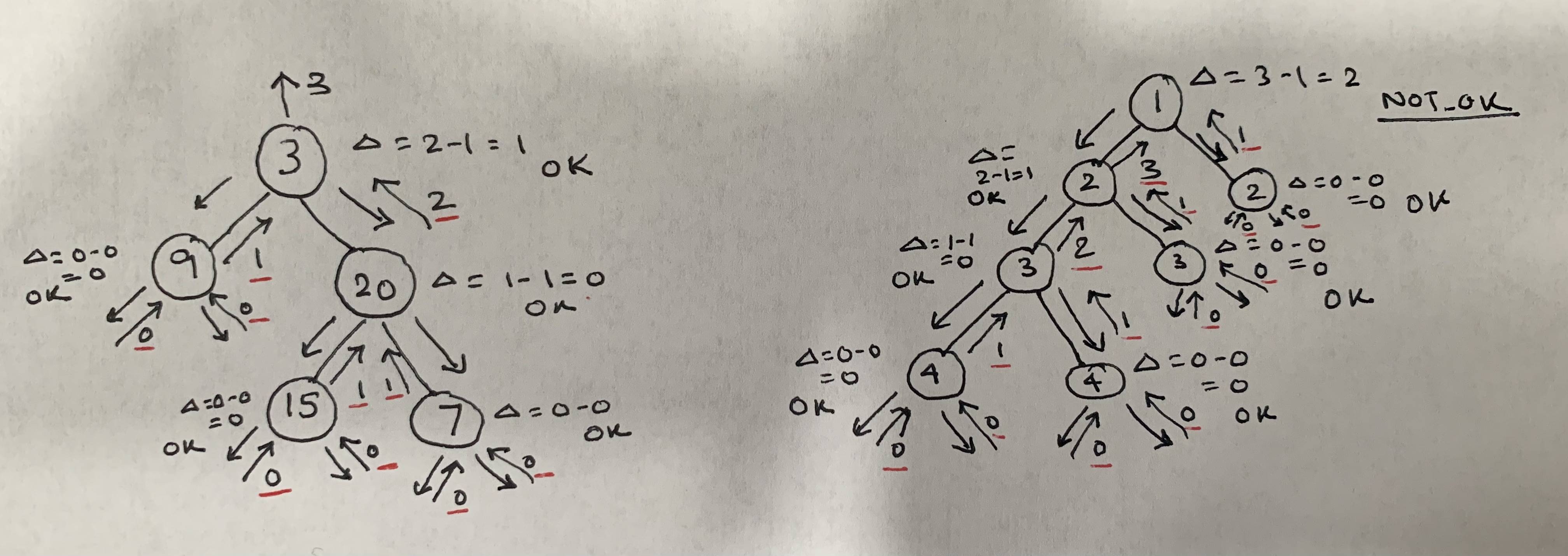

CodePudding user response：

few things to note:

• a tree height is the deepest level to its leaf.
• naturally, a parent height is the height of its tallest child 1.
• a tree is balanced if the difference between ALL its children heights is 1 or less.
• the function name treeHeight is confusing. should be called balancedTreeHeightOrMinusOne

so a tree is balanced if balancedTreeHeightOrMinusOne is not -1; it is calculated by checking (recursively) the balancedTreeHeightOrMinusOne of its children. if the diff between them is too big then return -1 for this is not balanced. Otherwise return the height of it's tallest children plus one.

CodePudding user response：

The base case is this:

if(!root) return 0;

So we know how the function could return 0.

The next case to look at is this one:

return Math.max(leftSubTree, rightSubTree)   1;

We know from the base case that both leftSubTree and rightSubTree could be 0 (since they represent a return value from a recursive call), and so we then have a case here where 1 is returned. So now we have seen that either 0 or 1 could be returned.

But then this return could also get a maximum that is 1, and so return 2! And so any positive integer becomes a possible return value.

Now look at this statement:

if(Math.abs(leftSubTree - rightSubTree) > 1) return -1; 

As we saw that leftSubTree and rightSubTree could be any unsigned integer (since they are the values returned by a recursive call), the absolute difference can be any unsigned integer, and so there can be cases where this condition is true. So now we have a first case where the returned value is -1 (which here means: "it is not balanced").

The only statement that remains to be explained:

if(leftSubTree === -1 || rightSubTree === -1) return -1;

In the previous case we saw that indeed a recursive call can return -1. So here it says that if either subtree is not balanced then this tree is not balanced either.

CodePudding user response：

Suppose you have a simple tree like:

const tree = {
  val: 1,
  left: null,
  right: {
    val: 2,
    left: null,
    right: null
  }
}

When you call treeHeight(tree), you get two recursive calls: treeHeight(tree.left) and treeHeight(tree.right).

Since tree.left is null, treeHeight(tree.left) returns 0, so leftSubtree == 0.

tree.right is not null, so it recurses again, calling treeHeight(tree.right.left and treeHeight(tree.right.right). Since both of these are null, both return values are 0, so in this call, leftSubtree == 0 and rightSubtree == 0. Math.abs(leftSubTree - rightSubTree) == 0, so it returns Math.max(leftSubtree, rightSubtree) 1. Since Math.max(0, 0) is 0, this returns 1.

So in the original call, we now have rightSubtree == 1. Math.abs(leftSubTree - rightSubTree) > 1) == 1, so the condition Math.abs(leftSubTree - rightSubTree) > 1) fails. We go to the else block and return Math.max(leftSubtree, rightSubtree) 1. This returns 2.