Excel Dynamic Solution for Cumulated Product / Running Product of an Array without SCAN or OFFSET-CodePudding

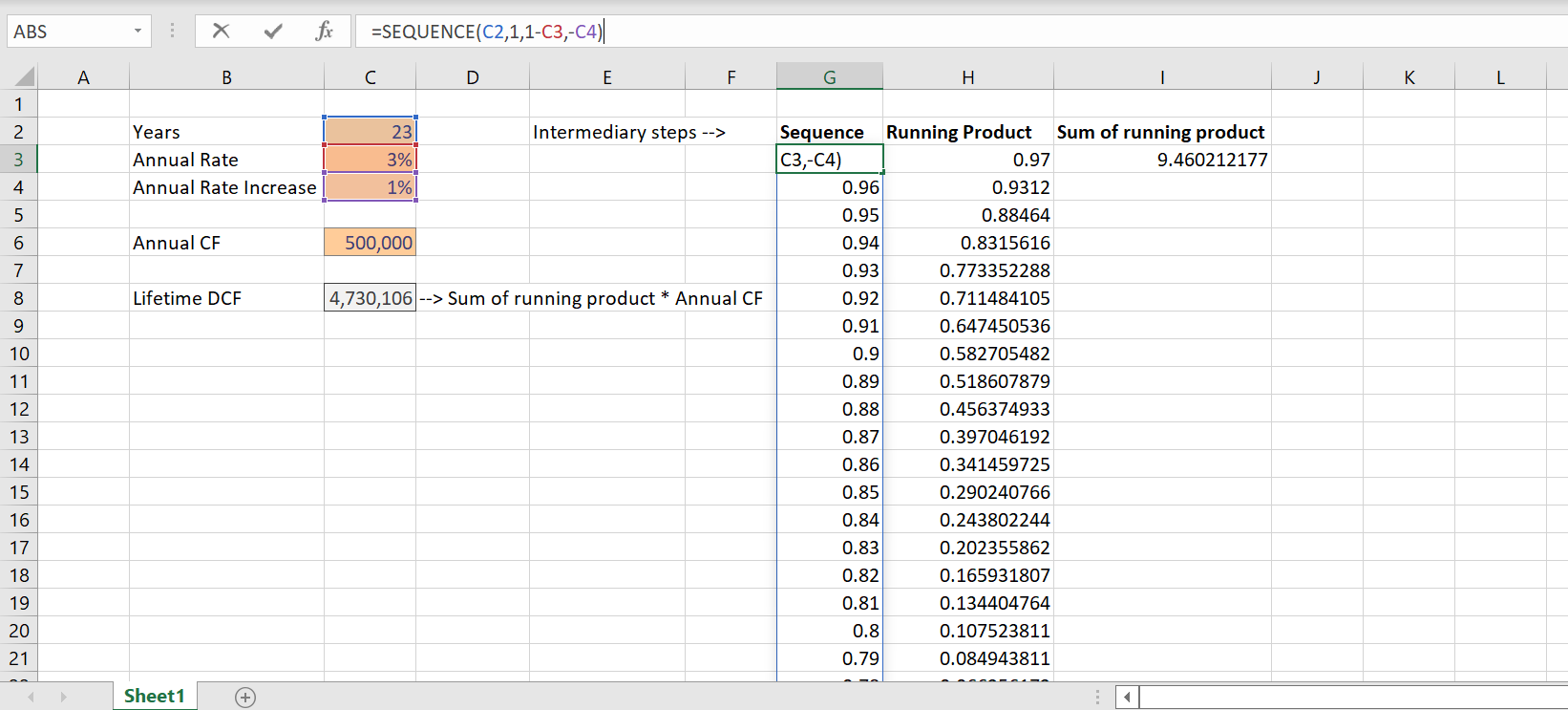
I want to calculate the cumulated / running product of an array.

However, the solutions provided under these two questions are not quite what I want:

CodePudding user response：

Modifying the OP's question starting formula from the

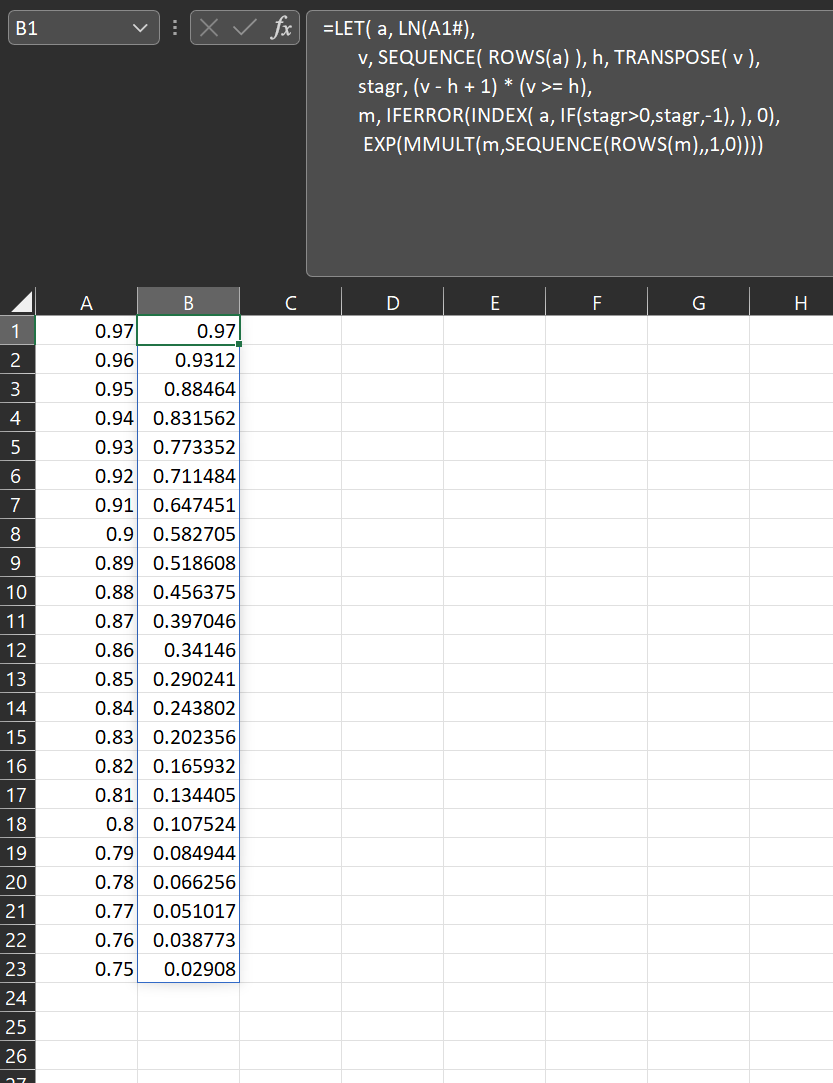
You should be able to replace the A1# with your SEQUENCE formula:
```
=LET( a, LN(SEQUENCE(D11,1,1-D23,D24)),
       v, SEQUENCE( ROWS(a) ), h, TRANSPOSE( v ),
       stagr, (v - h   1) * (v >= h),
       m, IFERROR(INDEX( a, IF(stagr>0,stagr,-1), ), 0),
        EXP(MMULT(m,SEQUENCE(ROWS(m),,1,0))))
```
CodePudding user response：

Based on your initial formulation and requirements. On F2 you can put the following formula. Since you can use SEQUENCE I assume you can use LET too.
```
=LET(n, B2, seq,LOG10(SEQUENCE(n,1,1-B3,B4)), seqInc, INT(SEQUENCE(n,n,0)/n) 1, 
 LUnitTriMatrix, --(seqInc >= TRANSPOSE(seqInc)), mult,
 MMULT(LUnitTriMatrix, seq), POWER(10, mult))
```
This solution doesn't require to create a range with the sequence, instead it just uses the array generated based on sequence input parameters.

Here is the output:

Note: Columns Sequence and Manual are just for testing purpose.

Explanation

The solution uses the following two main ideas:

IDEA 1: The solution suggested in the answer provided by @Alister of the question you shared as a reference: Excel Dynamic Array formula to create a running product of a column. The idea is to use the following logarithm property:
```
log(a*b) = log(a)   log(b)
```
therefore
```
a*b = exp(log(a*b)) = exp(log(a)   log(b))
```
so we convert a product cumulated problem into a sum cumulated problem of log items. We finally apply the inverse operation (exponential) to obtain the corresponding cumulative product.

IDEA2: To build Lower Unitary Triangular Matrix (LUnitTriMatrix for future reference) so we can use a matrix multiplication via MMULT. For example:
```
|1 0 0|   |a|    |a         |
|1 1 0| x |b|  = |a   b     |
|1 1 1|   |c|    |a   b   c |
```
The LUnitTriMatrix can be obtained via the following two sequences:
```
 seqInc, INT(SEQUENCE(n,n,0)/n) 1
```
for n equal 5 for example the output is:
```
|1 1 1 1 1|
|2 2 2 2 2|
|3 3 3 3 3|
|4 4 4 4 4| 
|5 5 5 5 5|
```
and the corresponding transpose matrix: TRANSPOSE(seqInc):

The following condition generates the desired matrix:
```
LUnitTriMatrix, --(seqInc >= TRANSPOSE(seqInc))
```
For example:
```
|1 1 1 1 1 1|    |1 2 3 4 5|   |1 0 0 0 0|
|2 2 2 2 2 2|    |1 2 3 4 5|   |1 1 0 0 0| 
|3 3 3 3 3 3| >= |1 2 3 4 5| = |1 1 1 0 0|
|4 4 4 4 4 4|    |1 2 3 4 5|   |1 1 1 1 0|
|5 5 5 5 5 5|    |1 2 3 4 5|   |1 1 1 1 1|
```
The rest is just to do the multiplication:
```
mult, MMULT(LUnitTriMatrix, seq)
```
and the inverse operation (power of ten): POWER(10, mult)

Explanation