I'm trying to test if lines can be placed by seeing if they would intersect with any existing lines in a list.
public static bool onLine(Line l1, Vector2 p)
{ //check whether p is on the line or not
if (p.x <= Mathf.Max(l1.startingPoint.x, l1.endingPoint.x) && p.x <= Mathf.Min(l1.startingPoint.x, l1.endingPoint.x) &&
(p.y <= Mathf.Max(l1.startingPoint.y, l1.endingPoint.y) && p.y <= Mathf.Min(l1.startingPoint.y, l1.endingPoint.y)))
return true;
return false;
}
public static int directionV2(Vector2 a, Vector2 b, Vector2 c)
{
float val = (b.y - a.y) * (c.x - b.x) - (b.x - a.x) * (c.y - b.y);
if (val == 0)
return 0; //colinear
else if (val < 0)
return 2; //anti-clockwise direction
return 1; //clockwise direction
}
public static bool isIntersect(Line l1, Line l2)
{
//four direction for two lines and points of other line
int dir1 = directionV2(l1.startingPoint, l1.endingPoint, l2.startingPoint);
int dir2 = directionV2(l1.startingPoint, l1.endingPoint, l2.endingPoint);
int dir3 = directionV2(l2.startingPoint, l2.endingPoint, l1.startingPoint);
int dir4 = directionV2(l2.startingPoint, l2.endingPoint, l1.endingPoint);
if (dir1 != dir2 && dir3 != dir4)
return true; //they are intersecting
if (dir1 == 0 && onLine(l1, l2.startingPoint)) //when p2 of line2 are on the line1
return true;
if (dir2 == 0 && onLine(l1, l2.endingPoint)) //when p1 of line2 are on the line1
return true;
if (dir3 == 0 && onLine(l2, l1.startingPoint)) //when p2 of line1 are on the line2
return true;
if (dir4 == 0 && onLine(l2, l1.endingPoint)) //when p1 of line1 are on the line2
return true;
return false;
}
public struct Line
{
public Vector2 startingPoint;
public Vector2 endingPoint;
public Line(Vector2 start, Vector2 end)
{
this.startingPoint = new Vector2(start.x, start.y);
this.endingPoint = new Vector2(end.x, end.y);
}
}
This is what I've managed to gather so far through other posts but I'm struggling adjusting it to include that two lines can share the same starting position without it being intersecting.
Update: I figured that adding the conditions l1.startingPoint != p && l1.endingPoint != p would be the solution. The code however seems to still be producing intersecting lines. I'm uncertain if my solution is wrong or if I'm creating the issue in a different part of code.
Update Update: included Line struct
Any help would be greatly appreciated.
CodePudding user response:
Intersection test between two line segments
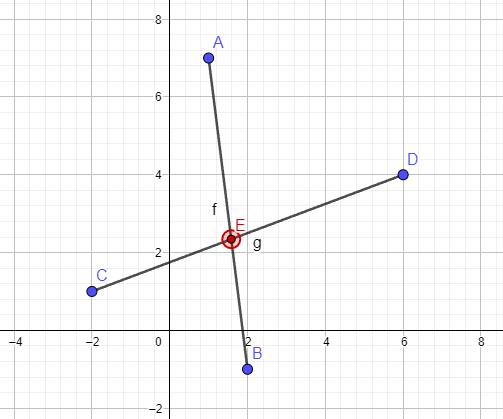
Segment A: [<1, 7>-<2, -1>]
Segment B: [<-2, 1>-<6, 4>]
Segments A, B intersect at <1.58209, 2.343284>.
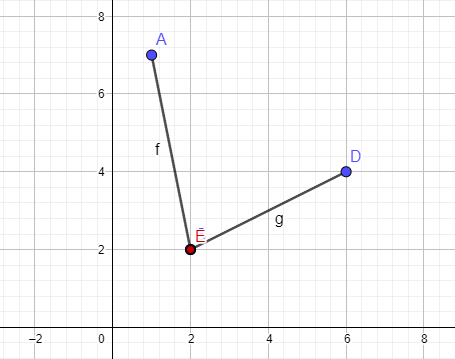
Segment A: [<1, 7>-<2, -1>]
Segment B: [<2, 2>-<6, 4>]
Segments A, B do not intersect.
Summary
There are two parts to this process.
Extend the lines to infinity and see where (and if) they intersect.
- Form the lines using
(a,b,c)coordinates with equationsa*x b*y c=0. These are the homogeneous coordinates of a line. - Find the homogeneous coordinates of the point where two lines meet.
- Form the lines using
Check if the intersection point is contained within a line segment.
- Project the point on the line. This step can be omitted in this case because by definition the point is common to both lines.
- Find the distance ratio
tof the point along the distanceAtoB. Ift=0then the point is atA, ift=100%then the point is atBand ift=50%then the point is at the midpoint ofAB. The point is contained in the segment ift>=0andt<=1.
Note on nomenclature. A line is an infinite line, and a line segment is the line defined between two points.
Details
The crux of the procedure above is implemented inside the LineeSegment.TryIntersect() method.
Program
The use used to generate the tests above. GeometryTools is a static class containing helpful methods and values.
class Program
{
static void Main(string[] args)
{
var segA = new LineSegment(
new Vector2(1, 7),
new Vector2(2, -1));
var segB = new LineSegment(
new Vector2(-2, 1),
new Vector2(6, 4));
Console.WriteLine($"Segment A: {segA}");
Console.WriteLine($"Segment B: {segB}");
if (segA.TryIntersect(segB, out Vector2 point))
{
Console.WriteLine($"Segments A, B intersect at {point}.");
}
else
{
Console.WriteLine($"Segments A, B do not intersect.");
}
}
}
Line Segment
The code above depends on a class LineSegment that is defined from two points, and the function TryIntersect() which checks if two line segments intersect.
public readonly struct LineSegment
{
public LineSegment(Vector2 from, Vector2 to) : this()
{
From = from;
To = to;
}
public Vector2 From { get; }
public Vector2 To { get; }
public float Length { get => Vector2.Distance(From, To); }
public Vector2 Direction { get => Vector2.Normalize(To - From); }
public Vector2 Normal { get => Vector2.Normalize(new Vector2(-(To.Y - From.Y), (To.X - From.X))); }
public bool IsFinite
{
get => !float.IsNaN(From.X) && !float.IsNaN(From.Y)
&& !float.IsNaN(To.X) && !float.IsNaN(To.Y);
}
/// <summary>
/// Check if a point is contained within the line segment
/// </summary>
/// <param name="target"></param>
/// <returns></returns>
public bool Contains(Vector2 target, bool inclusive = true)
{
if (TryJoin(From, To, out var line))
{
target = line.Project(target);
Vector2 dir = Direction;
float t = Vector2.Dot(dir, target - From) / Vector2.Dot(dir, To - From);
return inclusive ? t >= 0 && t <= 1 : t > TINY && t < 1 - TINY;
}
return false;
}
/// <summary>
/// Try to intersect two line segments
/// </summary>
/// <param name="other">The other line segment.</param>
/// <param name="point">The intersection point.</param>
/// <returns>True if they intersect, False otherwise</returns>
public bool TryIntersect(LineSegment other, out Vector2 point, bool inclusive = true)
{
point = Vector2.Zero;
if (GeometryTools.TryJoin(From, To, out InfiniteLine thisLine)
&& GeometryTools.TryJoin(other.From, other.To, out InfiniteLine otherLine))
{
if (GeometryTools.TryMeet(thisLine, otherLine, out point))
{
return Contains(point, inclusive) && other.Contains(point, inclusive);
}
}
return false;
}
public override string ToString() => $"[{From}-{To}]";
}
Infinite Line
It is helpful to group the parameters and properties of an infinte line into a class.
public readonly struct InfiniteLine
{
/// <summary>
/// The line at the horizon (not on the Eucledian plane).
/// </summary>
public static readonly InfiniteLine Horizon = new InfiniteLine(0, 0, 1);
public InfiniteLine(float a, float b, float c) : this()
{
this.Coeff = (a, b, c);
float m = (float)Math.Sqrt(a * a b * b);
this.IsFinite = m > GeometryTools.TINY;
}
/// <summary>
/// The (a,b,c) coefficients define a line by the equation: <code>a*x b*y c=0</code>
/// </summary>
public (float a, float b, float c) Coeff { get; }
/// <summary>
/// True if line is in finite space, False if line is at horizon.
/// </summary>
public bool IsFinite { get; }
/// <summary>
/// Check if point belongs to the infinite line.
/// </summary>
/// <param name="point">The target point.</param>
/// <returns>True if point is one the line.</returns>
public bool Contains(Vector2 point)
{
return IsFinite
&& Math.Abs(Coeff.a * point.X Coeff.b * point.Y Coeff.c) <= TINY;
}
/// <summary>
/// Projects a target point onto the line.
/// </summary>
/// <param name="target">The target point.</param>
/// <returns>The point on the line closest to the target.</returns>
/// <remarks>If line is not finite the resulting point has NaN or Inf coordinates.</remarks>
public Vector2 Project(Vector2 target)
{
(float a, float b, float c) = Coeff;
float m2 = a * a b * b;
float px = b * (b * target.X - a * target.Y) - a * c;
float py = a * (a * target.Y - b * target.X) - b * c;
return new Vector2(px / m2, py / m2);
}
public override string ToString() => $"({Coeff.a})*x ({Coeff.b})*y ({Coeff.c})=0";
}
Geometry Tools
Helper function that define a line from two points (meet), or define a point from two lines (join). But in Euclidian geometry these operations might fail (parallel lines, or coincident points) so they are designed here to return true/false values accordingly.
public static class GeometryTools
{
/// <summary>
/// The value of 2^-19 is tiny
/// </summary>
public const float TINY = 1f / 524288;
/// <summary>
/// Try to join two points with an infinite line.
/// </summary>
/// <param name="A">The first point.</param>
/// <param name="B">The second point.</param>
/// <param name="line">The line joining the two points.</param>
/// <returns>False if the two points are coincident, True otherwise.</returns>
public static bool TryJoin(Vector2 A, Vector2 B, out InfiniteLine line)
{
float dx = B.X - A.X, dy = B.Y - A.Y;
float m = A.X * B.Y - A.Y * B.X;
line = new InfiniteLine(-dy, dx, m);
return line.IsFinite;
}
/// <summary>
/// Try to find the point where two infinite lines meet.
/// </summary>
/// <param name="L">The fist line.</param>
/// <param name="M">The second line.</param>
/// <param name="point">The point where the two lines meet.</param>
/// <returns>False if the two lines are parallel, True othrwise.</returns>
public static bool TryMeet(InfiniteLine L, InfiniteLine M, out Vector2 point)
{
(float a1, float b1, float c1) = L.Coeff;
(float a2, float b2, float c2) = M.Coeff;
float d = a1 * b2 - a2 * b1;
if (d != 0)
{
point = new Vector2((b1 * c2 - b2 * c1) / d, (a2 * c1 - a1 * c2) / d);
return true;
}
point = Vector2.Zero;
return false;
}
}
Exclude End Points
If by default the Contains() and TryIntersect() methods include the end points in the calculations. But with the opional parameter set to inclusive = false you can exclude end points.
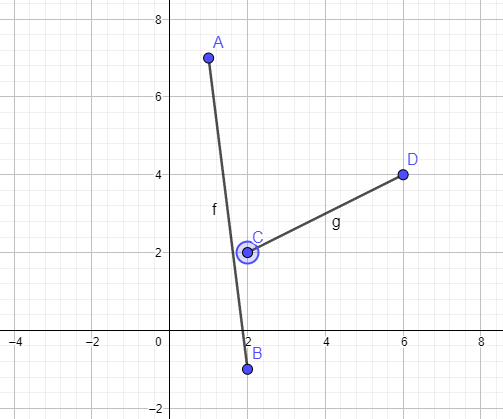
static void Main(string[] args)
{
var segA = new LineSegment(
new Vector2(1, 5),
new Vector2(2, 2));
var segB = new LineSegment(
new Vector2(2, 2),
new Vector2(6, 4));
Console.WriteLine($"Segment A: {segA}");
Console.WriteLine($"Segment B: {segB}");
if (segA.TryIntersect(segB, out Vector2 point, false))
{
Console.WriteLine($"Segments A, B intersect at {point}.");
}
else
{
Console.WriteLine($"Segments A, B do not intersect.");
}
}
}
See the example below
with output
Segment A: [<1, 5>-<2, 2>]
Segment B: [<2, 2>-<6, 4>]
Segments A, B do not intersect.
This means that you can use A.TryIntersect(B, out var point, false) to specify if endpoints would count as a collision or not.
The code above is far from optimized as it calls several functions many times over and over, instead of caching the results and using them. It is for illustrative purposes to explain the process step by step.