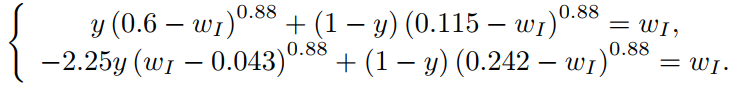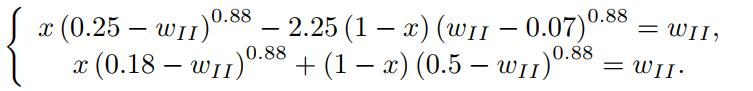2 unknown equations raise NotImplementedError-CodePudding

I have these 2 unknown equations problem(technically 4, two pairs)

The results should be these or close to them:

wI = 0.107 ∈ (a1, a2) , y= 0.176.

wII = 0.123 ∈ (b1, b2) , x= 0.877.

I wrote for each of them 2 types of solver, the first one is the case where the equations are equal to zero and the second when they are equal to ww1/ww2. In every case the program raise

NotImplementedError('could not solve %s' % eq2)

and

NotImplementedError: could not solve: -5*2**(4/5)*2**(24/25)*5**(19/25)*ww2   5*80000000000000000000**(1/25)*(1 - 2*ww2)**(22/25)*(-(40*10**(19/25)*ww2 - 9*(100*ww2 - 7)**(22/25))/(20*5**(19/25)*(1 - 4*ww2)**(22/25) - 9*(100*ww2 - 7)**(22/25))   1)   2**(22/25)*(9 - 50*ww2)**(22/25)*(40*10**(19/25)*ww2 - 9*(100*ww2 - 7)**(22/25))/(20*5**(19/25)*(1 - 4*ww2)**(22/25) - 9*(100*ww2 - 7)**(22/25))

error message and I don't know why or where is the problem.

Thanks in advance for the help.

import nashpy as nash
import numpy as np
import math
from sympy import symbols, Eq, solve

a4 = 0.6
a3 = 0.242
a2 = 0.115
a1 = 0.043
b4 = 0.5
b3 = 0.25
b2 = 0.18
b1 = 0.07

alpha = 0.88
beta = alpha
LambdaI = 2.25
LambdaII = LambdaI
Mu = alpha
Nu = alpha

y,ww1=symbols('y ww1')
eq3=Eq((y*pow((a4-ww1),alpha) (1-y)*pow((a2-ww1),alpha)-ww1),0)
eq4=Eq(((-1)*LambdaI*y*pow((ww1-a1),beta) (1-y)*pow((a3-ww1),alpha)-ww1),0)
print(solve((eq3,eq4), (y, ww1)))

y,ww1=symbols('y ww1')
eq3=Eq((y*pow((a4-ww1),alpha) (1-y)*pow((a2-ww1),alpha)),ww1)
eq4=Eq(((-1)*LambdaI*y*pow((ww1-a1),beta) (1-y)*pow((a3-ww1),alpha)),ww1)
print(solve((eq3,eq4), (y, ww1)))



x,ww2=symbols('x ww2')
eq5=Eq((x*pow((b3-ww2),Nu)-(-1)*LambdaII*(1-x)*pow((ww2-b1),Nu)),ww2)
eq6=Eq((x*pow((b2-ww2),Nu) (1-x)*pow((b4-ww2),Nu)),ww2)
print(solve((eq5,eq6), (x, ww2)))

x,ww2=symbols('x ww2')
eq5=Eq((x*pow((b3-ww2),Nu)-(-1)*LambdaII*(1-x)*pow((ww2-b1),Nu)-ww2),0)
eq6=Eq((x*pow((b2-ww2),Nu) (1-x)*pow((b4-ww2),Nu)-ww2),0)
print(solve((eq5,eq6), (x, ww2)))

CodePudding user response：

Based on your 'results', it seems like you're looking for a numeric solution - so Sympy is the wrong tool for the job. Do a bounded, numeric, non-linear minimization of a scalar least-squares cost. Many of the Scipy methods work; slsqp converges quickly, powell is a little more accurate:

import numpy as np
from scipy.optimize import minimize

a1, a2, a3, a4 = 0.043, 0.115, 0.242, 0.600
b1, b2, b3, b4 = 0.070, 0.180, 0.250, 0.500
alpha = beta = Mu = Nu = 0.88
LambdaI = LambdaII = 2.25


def eq34(params: np.ndarray) -> float:
    ww1, y = params
    err3 = ww1 - (1 - y)*(a2 - ww1)**Mu - y*(a4 - ww1)**Mu
    err4 = ww1 - (1 - y)*(a3 - ww1)**Mu   y*(ww1 - a1)**Mu*LambdaI
    return err3*err3   err4*err4


def eq56(params: np.ndarray) -> float:
    ww2, x = params
    err6 = ww2 - x*(b2 - ww2)**Nu - (1 - x)*(b4 - ww2)**Nu
    err5 = ww2 - x*(b3 - ww2)**Nu   (1 - x)*(ww2 - b1)**Nu*LambdaII
    return err5*err5   err6*err6


print(minimize(
    fun=eq34, method='powell', tol=1e-18,  # l-bfgs-b, powell or slsqp work well
    x0=((a1   a2)/2, 0),
    bounds=((a1, a2), (None, None)),
))
print()

print(minimize(
    fun=eq56, method='powell', tol=1e-18,
    x0=((b1   b2)/2, 0),
    bounds=((b1, b2), (None, None)),
))

   direc: array([[0.00000000e 00, 1.00000000e 00],
       [8.19680836e-06, 7.76203141e-06]])
     fun: 7.703719777548943e-34
 message: 'Optimization terminated successfully.'
    nfev: 181
     nit: 5
  status: 0
 success: True
       x: array([0.10667594, 0.17596731])

   direc: array([[ 0.00000000e 00,  1.00000000e 00],
       [-8.68955012e-10, -5.86052659e-11]])
     fun: 2.0928706714135016e-27
 message: 'Optimization terminated successfully.'
    nfev: 155
     nit: 4
  status: 0
 success: True
       x: array([0.12265264, 0.87814778])