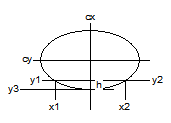
How to calculate the bounding box of an axis aligned ellipse for given centerpoint cx,cy and an axis aligned intersection line with endpoints x1y1 and x2y2 at distance h from a bound ?

My purpose is to draw part of an ellipse, using the win32 Chord function.

CodePudding user response：

Having an axis-aligned ellipse means we just need to find the values for our major and minor radii, after which we know our bounding box, since that'll be a box with width 2b, height 2a, and center (h,k) (using the letters that maths uses when describing ellipses). And of course, once we have those, we can trivially derive the corner points if we need minx/miny/maxx/maxy coordinates instead.

So, the formula for an ellipse centered at (h, k) is:

 (x-h)²    (y-k)²
───────   ─────── = 1
   a²        b²

and from your diagram we know h = cx, k = cy, a = y3 - h, and we know not just one, but three points on our ellipse. That leaves us needing to find one unknown, which is pretty easy: using x = x1 - cx and y = y1 - cy, we solve for b and get

          ay
b = ± ─̲─̲─̲─̲─̲─̲─̲─̲─̲──
      ⎷│a² - x²│

And we're done. We have all the values we need to build that AAB box now.