How do I find the intersection of more than two polynomial curves?-CodePudding

I have four polynomial (degree 2) functions and I need to find the intersection of these functions. but I do not know is any way to find all intersections in one step. my suggestion is to equalize two functions and find their roots using numpy.roots. but I am not sure if is it true or not. what should I do to find the intersections? my functions are:

y = 1.51250 * x   -0.07969 * x^2   18.96116
y = 1.54264 * x   -0.05879 * x^2   17.47277
y = 1.49669 * x   -0.04627 * x^2   17.69008
y = 1.72147 * x   0.00052 * x^2   18.21067

I equal two first equations to find their roots, we will have :

-0.03014x-0.0209x^2 1.48839=0

I used np.roots to find the roots:

coeff=[-0.03014,-0.0209,1.48839]
np.roots(coeff)

the roots are:

[-7.38253508, 6.68910443]

but when I put each of these roots in this equation -0.03014x-0.0209x^2 1.48839=0 the output is not zero! what is the problem?

CodePudding user response：

If a single point exists at which all four curves have the same value, then it should be possible to find the intersections of any one of the curves will each of the other three, and of the resulting intersection, you'd pick the one that's common among them all. I can't think of a "one-step" way to do it besides that. As for finding the intersections between each pair of curves, here's how I would do it:

import numpy as np
from numpy.polynomial import Polynomial as Poly


from matplotlib import pyplot as plt

# Your functions:
    
#     y = 1.51250 * x   -0.07969 * x^2   18.96116
#     y = 1.54264 * x   -0.05879 * x^2   17.47277
#     y = 1.49669 * x   -0.04627 * x^2   17.69008
#     y = 1.72147 * x   0.00052 * x^2   18.21067

y1 = Poly((18.96116, 1.51250, -0.07969))
y2 = Poly((17.47277, 1.54264, -0.05879))
y3 = Poly((17.69008, 1.49669, -0.04627))
y4 = Poly((18.21067, 1.72147, -0.00052))


# Showing how to find intersections between y1 and y2 only
# you could repeat this for other combinations as you please:
y1_y2_intersections = (y1-y2).roots()

# This returns the two x values at which the functions y1 and y2 have the same value

# Plotting the curves and their intersections:

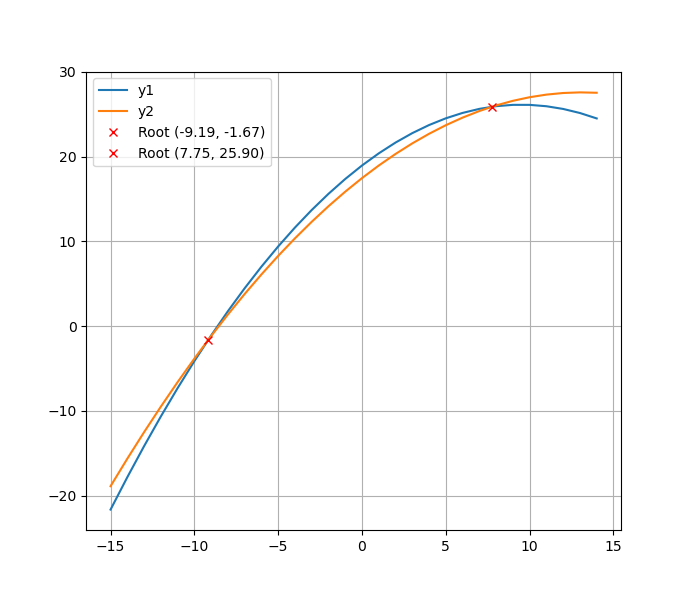
x = np.arange(-15, 15) 

fig, ax = plt.subplots()

ax.plot(x, y1(x), label = 'y1') # Plotting y1
ax.plot(x, y2(x), label = 'y2') # Plotting y2

# Plotting the intersection points

for x, y in zip(y1_y2_intersections, y1(y1_y2_intersections)):
    ax.plot(x, y, marker = 'x', color = 'red', linestyle = 'None', label = f'Root ({x:.2f}, {y:.2f})')
    
ax.grid()
ax.legend()

Produces this:

CodePudding user response：

You can equalize any two polynomials and solve the resulting quadratic equations. There is, of course, a solution for any of these equations. Maybe the some (or all) of them are imaginary or complex. Just ignore these solutions if you want to use only real solutions for your intended purpose.

CodePudding user response：

For equation

-0.03014x-0.0209x^2 1.48839=0

coefficients should be in correct order

coeff=[-0.0209, -0.03014,1.48839]

and result for

np.roots(coeff)

[-9.19068954  7.74858428]