Measure integral between 2 curves (linear func & arbitrary curve)-CodePudding

In the img. below my goal is to locate the integral in area 1 / 2 / 3. In that way that I know how much area below the linear line (area 1 / 3), and how much area that are above the linear line (area 2)

Im not looking for the exact integral, just an approximately value to measure on. an approx that would work in the same fashion for other version of the curves I have represented.

y1: The blue line is a linear function y= -0.148x 1301.35

y2:The yellow line is a arbitrary curve

Both curves share the same x axis.

image of curves linear & arbitrary curve

I have tried several methods, found here on stackoverflow, mainly theese 2 methods cought my attention:

https://stackoverflow.com/a/57827807

https://stackoverflow.com/a/25447819

They give me the exact same output for the whole area, my issue is to seperate it above / below.

Example of my best try: (Modified version of https://stackoverflow.com/a/25447819/20441461)

y1 / y2 / x - is the data used for the curves in the img. above

y1 = [1298.54771845, 1298.40019417, 1298.2526699, 1298.10514563, 
     1297.95762136,1297.81009709, 1297.66257282, 1297.51504854]

y2 = [1298.59, 1297.31, 1296.04, 1297.31, 1296.95, 1299.18, 1297.05, 1297.45]

x = np.arange(len(y1))

z = y1-y2
dx = x[1:] - x[:-1]
cross_test = np.sign(z[:-1] * z[1:])

x_intersect = x[:-1] - dx / (z[1:] - z[:-1]) * z[:-1]
dx_intersect = - dx / (z[1:] - z[:-1]) * z[:-1]

areas_pos = abs(z[:-1]   z[1:]) * 0.5 * dx # signs of both z are same   
areas_neg = 0.5 * dx_intersect * abs(z[:-1])   0.5 * (dx - dx_intersect) * abs(z[1:])

negatives = np.where(cross_test < 0)
negative_sum = np.sum(x_intersect[negatives])

positives = np.where(cross_test >= 0)
positive_sum = np.sum(x_intersect[positives])`

is give me this result:

Negative integral = 10.15

Positive integral = 9.97

Just from looking at the picture, I can tell that can not be the correct value. ( there is alot more area below the linear line than above.)

I have spend loads of time now on this, and are quite stuck - any advise or suggestion are welcome.

CodePudding user response：

Perhaps you can integrate the absolute difference of both arrays:

>>> np.trapz(np.abs(y2 - y1))
7.1417718350001

CodePudding user response：

Here is a little bit of code that calculates exactly all the areas, and does so in a vectorized way (fast):

def areas(x, y1, y2, details=None):
    dy = y1 - y2
    b0 = dy[:-1]
    b1 = dy[1:]
    b = np.c_[b0, b1]
    r = np.abs(b0) / (np.abs(b0)   np.abs(b1))
    rr = np.c_[r, 1-r]
    dx = np.diff(x)
    h = rr * dx[:, None]
    br = (b * rr[:, ::-1]).sum(1)
    a = (b   br[:, None]) * h / 2
    result = np.sum(a[a > 0]), np.sum(a[a < 0])
    if details is not None:
        details.update(locals())  # for debugging
    return result

Example:

x = np.array([0,1,2])
y1 = np.array([1,0,3])
y2 = np.array([0,3,4])

>>> areas(x, y1, y2)
(0.125, -3.125)

Your original example:

y1 = np.array([
    1298.54771845, 1298.40019417, 1298.2526699, 1298.10514563, 
    1297.95762136,1297.81009709, 1297.66257282, 1297.51504854])

y2 = np.array([1298.59, 1297.31, 1296.04, 1297.31, 1296.95, 1299.18, 1297.05, 1297.45])

x = np.arange(len(y1))

>>> areas(x, y1, y2)
(5.228440802728334, -0.8687563377282332)

Explanation

To understand how it works, let us consider the quadrilateral of four points: [a, b, c, d], where a and b are at the same x position, and so are c and d. It can be "straight" if none of the edges intersect, or "twisted" otherwise. In both cases, we consider the x-position of the intersection where the twisted version would intersect, and the actual vertical section of the quadrilateral at that position (0 if twisted, or the weighted average of the vertical sides if straight).

Say we call the vertical distances b0 and b1. They are oriented (positive if y1 > y2). The intersection is at x-coordinate x r * dx, where r = |b0| / (|b0| |b1|) and is a factor between 0 and 1.

For a twisted quad, the left (triangular) area is b0*r*dx/2 and the right one is b1*(1-r)*dx/2.

For a straight quad, the left area (trapeze) is (b0 br)/2 * r * dx and the right is (b1 br) / 2 * (1 - r) * dx, where br is the height at the r horizontal proportion, and br = b0 * (1 - r) b1 * r.

To generalize, we always use br in the calculation. For twisted quads, it is 0 and we can use the same expression as for straight quads. This is the key to eliminate any tests and produce a pure vectorized function.

The rest is a bit of numpy expressions to calculate all these values efficiently.

Example detail

def plot_details(details, ax=None):
    x, y1, y2, dx, r, a = [details[k] for k in 'x y1 y2 dx r a'.split()]
    ax = ax if ax else plt.gca()
    ax.plot(x, y1, 'b.-')
    ax.plot(x, y2, 'r.-')
    xmid = x[:-1]   dx * r
    [ax.axvline(xi) for xi in xmid]
    xy1 = np.c_[x, y1]
    xy2 = np.c_[x, y2]
    for A,B,C,D,r,(a0,a1) in zip(xy1, xy2, xy1[1:], xy2[1:], r, a):
        ACmid = A*(1-r)   C*r
        BDmid = B*(1-r)   D*r
        q0 = np.c_[A,ACmid,BDmid,B]
        q1 = np.c_[ACmid,C,D,BDmid]
        ax.fill(*q0, alpha=.2)
        ax.fill(*q1, alpha=.2)
        ax.text(*q0.mean(1), f'{a0:.3f}', ha='center')
        ax.text(*q1.mean(1), f'{a1:.3f}', ha='center')

Taking the earlier example:

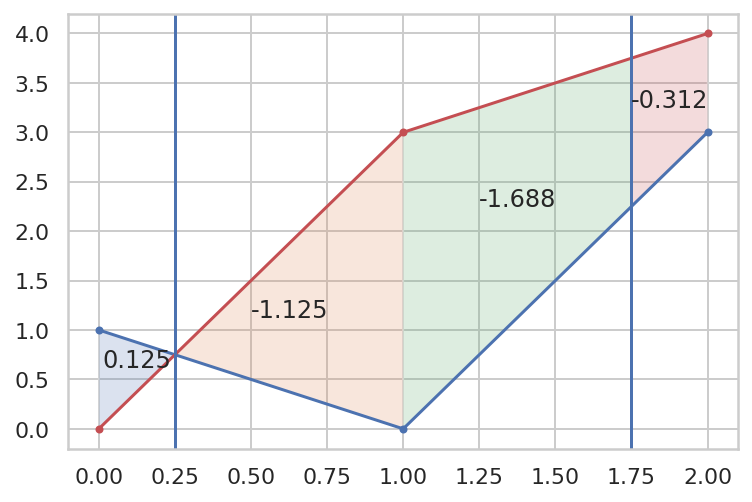
x = np.array([0,1,2])
y1 = np.array([1,0,3])
y2 = np.array([0,3,4])

details = {}
>>> areas(x, y1, y2, details)
(0.125, -3.125)

>>> details
{'x': array([0, 1, 2]),
 'y1': array([1, 0, 3]),
 'y2': array([0, 3, 4]),
 'details': {...},
 'dy': array([ 1, -3, -1]),
 'b0': array([ 1, -3]),
 'b1': array([-3, -1]),
 'b': array([[ 1, -3],
        [-3, -1]]),
 'r': array([0.25, 0.75]),
 'rr': array([[0.25, 0.75],
        [0.75, 0.25]]),
 'dx': array([1, 1]),
 'h': array([[0.25, 0.75],
        [0.75, 0.25]]),
 'br': array([ 0. , -1.5]),
 'a': array([[ 0.125 , -1.125 ],
        [-1.6875, -0.3125]]),
 'result': (0.125, -3.125)}

And:

plot_details(details)