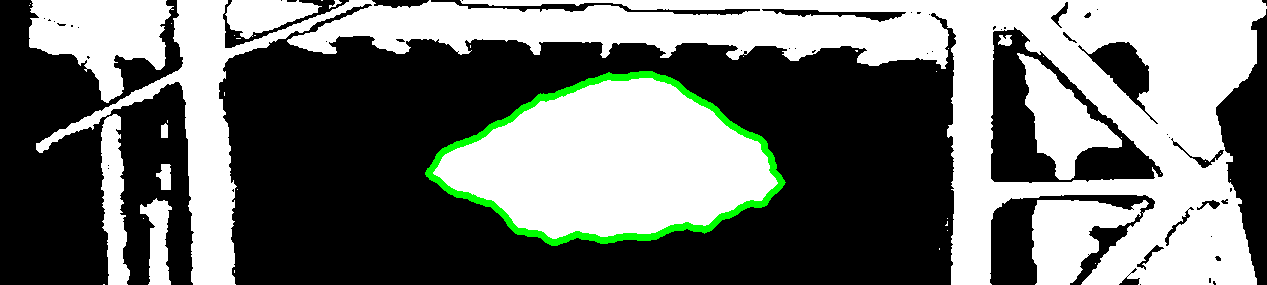
I am processing binary images, and was previously using this code to find the largest area in the binary image:

# Use the hue value to convert to binary
thresh = 20
thresh, thresh_img = cv2.threshold(h, thresh, 255, cv2.THRESH_BINARY)
cv2.imshow('thresh', thresh_img)
cv2.waitKey(0) 
cv2.destroyAllWindows()                        
# Finding Contours
# Use a copy of the image since findContours alters the image

contours, _ = cv2.findContours(thresh_img.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)

#Extract the largest area
c = max(contours, key=cv2.contourArea) 

This code isn't really doing what I need it to do, now I think it would better to extract the most central area in the binary image.

a cv.floodFill() on the center point can also quickly yield a labeling on that blob... assuming the mask is positive there. Otherwise, there needs to be search.

(cx, cy) = center.astype(int)
assert mask[cy,cx], "floodFill not applicable"

# trying cv.floodFill on the image center
mask2 = mask >> 1 # turns everything else gray
cv.floodFill(image=mask2, mask=None, seedPoint=center.astype(int), newVal=255)

# use (mask2 == 255) to identify that blob

This also takes less than a millisecond.

Some practically faster approaches might involve a pyramid scheme (low-res versions of the mask) to quickly identify areas of the picture that are candidates for an exact test (distance/intersection).

• Test target pixel. Hit (positive)? Done.
• Calculate low-res mask. Per block, if any pixel is positive, block is positive.
• Find positive blocks, sort by distance, examine closer all those that are within sqrt(2) * blocksize of the best distance.

CodePudding user response：

There are several ways you define "most central." I chose to define it as the region with the closest distance to the point you're searching for. If the point is inside the region, then that distance will be zero.

I also chose to do this with a pixel-based approach rather than a polygon-based approach, like you're doing with findContours().

Here's a step-by-step breakdown of what this code is doing.

1. Load the image, put it into grayscale, and threshold it. You're already doing these things.
2. Identify connected components of the image. Connected components are places where there are white pixels which are directly connected to other white pixels. This breaks up the image into regions.
3. Using np.argwhere(), convert a true/false mask into an array of coordinates.
4. For each coordinate, compute the Euclidean distance between that point and search_point.
5. Find the minimum within each region.
6. Across all regions, find the smallest distance.

import cv2
import numpy as np

img = cv2.imread('test197_img.png')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh_img = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
n_groups, comp_grouped = cv2.connectedComponents(thresh_img)
components = []
search_point = [600, 150]
for i in range(1, n_groups):
    mask = (comp_grouped == i)
    component_coords = np.argwhere(mask)[:, ::-1]
    min_distance = np.sqrt(((component_coords - search_point) ** 2).sum(axis=1)).min()
    components.append({
        'mask': mask,
        'min_distance': min_distance,
    })
closest = min(components, key=lambda x: x['min_distance'])['mask']

Output: