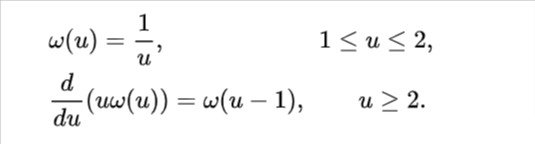How to solve a delay differential equation numerically-CodePudding

I would like to compute the

How can I compute this numerically efficiently?

CodePudding user response：

To get a general feeling of how DDE integration works, I'll give some code, based on the low-order Heun method (to avoid uninteresting details while still being marginally useful).

In the numerical integration the previous values are treated as a function of time like any other time-depending term. As there is not really a functional expression for it, the solution so-far will be used as a function table for interpolation. The interpolation error order should be as high as the error order of the ODE integrator, which is easy to arrange for low-order methods, but will require extra effort for higher order methods. The solve_ivp stepper classes provide such a "dense output" interpolation per step that can be assembled into a function for the currently existing integration interval.

So after the theory the praxis. Select step size h=0.05, convert the given history function into the start of the solution function table

u=1
u_arr = []
w_arr = []
while u<2 0.5*h:
    u_arr.append(u)
    w_arr.append(1/u)
    u  = h

Then solve the equation, for the delayed value use interpolation in the function table, here using numpy.interp. There are other functions with more options in `scipy.interpolate.

Note that h needs to be smaller than the smallest delay, so that the delayed values are from a previous step. Which is the case here.

u = u_arr[-1]
w = w_arr[-1]
while u < 4:
    k1 = (-w   np.interp(u-1,u_arr,w_arr))/u
    us, ws = u h, w h*k1
    k2 = (-ws   np.interp(us-1,u_arr,w_arr))/us
    u,w = us, w 0.5*h*(k1 k2)
    u_arr.append(us)
    w_arr.append(ws)

Now the numerical approximation can be further processed, for instance plotted.

plt.plot(u_arr,w_arr); plt.grid(); plt.show()