Replicating an ODE food-web model from a manuscript-CodePudding

I am trying to replicate a lake food web model published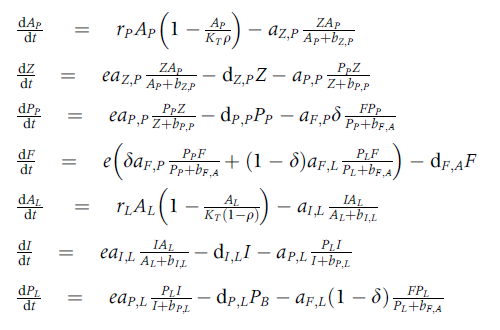

Here is my attempt at coding the model:

library(deSolve)

# define the model
vade_2005_model <- function(Time, State, Pars){
  
  with(as.list(c(State, Pars)), {

# pelagic components -----------------------------------------------

# resource
pel_res_dt <- (rPel * AP * (1 - (AP/(KT * q)))) - (aZP * ((Z * AP)/(AP   bZP)))

# zooplankton
pel_zoo_dt <-  (ef * aZP * ((Z * AP)/(AP   bZP))) - (dZP * Z) - (aPP * ((PP * Z)/(Z   bPP)))

# pelagic predator (PP)
pel_PP_dt <- (ef * aPP * ((PP * Z)/(Z   bPP))) - (dPP * PP) - (aFP * del * ((fish * PP)/(PP   bFA)))


# top predator - fish ---------------------------------------------
fish_dt <- (ef * ((del * aFP * ((PP * fish)/(PP * bFA)))   ((1 - del) * aFL * ((PL * fish)/(PL * bFA))))) - (dFA * fish)

# Littoral component -----------------------------------------------

# resource
lit_res_dt <- (rLit * AL * (1 - (AL/(KT * (1 - q))))) - (aIL * ((I * AL)/(AL   bIL)))

# littoral invert
lit_inv_dt <-  (ef * aIL * ((I * AL)/(AL   bIL))) - (dIL * I) - (aPL * ((PL * I)/(I   bPL)))

# littoral predator (PL)
lit_PL_dt <- (ef * aPL * ((PL * I)/(I   bPL))) - (dPL * PL) - (aFL * (1 - del) * ((fish * PL)/(PL   bFA)))

list(c(pel_res_dt, pel_zoo_dt, pel_PP_dt,
       fish_dt,
       lit_res_dt, lit_inv_dt, lit_PL_dt))
 })
}
  

# model parameters (taken from the manuscript)  
pars = c(rPel = 1.0,   # per capital growth rate of pelagic resource
         rLit = 0.8,   # per capital growth rate of littoral resource
         aZP = 1.55,    # Attack rate of zooplankton (in pelagic)
         aPP = 1.35,    # Attack rate of PP (in pelagic)
         aFP = 1.05,    # Attack rate of fish (in pelagic)
         aFL = 1.0,    # Attack rate of fish (in littoral)
         aIL = 1.45,    # Attack rate of invert (in littoral)
         aPL = 1.25,    # Attack rate of PL (in littoral)
         bZP = 0.2,    # Half saturation rate of zooplankton (in pelagic)
         bPP = 0.2,    # Half saturation rate of PP (in pelagic)
         bFA = 0.2,  # Half saturation rate of fish (in all)
         bIL = 0.2,    # Half saturation rate of invert (in littoral)
         bPL = 0.2,    # Half saturation rate of PL (in littoral)
         dZP = 0.6,    # biomass loss rate of zooplankton (in pelagic)
         dPP = 0.15,    # biomass loss rate of PP (in pelagic)
         dPL =  0.15,   # biomass loss rate of PL (in littoral)
         dIL = 0.6,    # biomass loss rate of invert (in littoral)
         dFA = 0.1,    # biomass loss rate of fish (all habitat)
         ef = 0.8,     # conversion efficiency of resource biomass into consumer biomass
         del = 0.5,    # fish preference (1 = PP, 0 = PL)
         KT = 1,    # lake carrying capacity
         q = 0.5    # prop. productivity in pelagic food chain
)      

# initial densities (assumed as not given in the manuscript)
yini <- c(AP = 0.5,
          Z = 0.5,
          PP = 0.5,
          fish = 0.5,
          AL = 0.5,
          I = 0.5,
          PL = 0.5
)

# time steps
times <- seq(0, 1000, by = 1)
  
# run model
out <- ode(yini, times, vade_2005_model, pars, method = "ode45")
out

If anyone can see where I have gone wrong it would be much appreciated!

CodePudding user response：

tl;dr there's a typo in your 'fish' equation (you multiplied instead of adding in the denominator). (I missed that you already said in your question that you had localized the problem to this equation! Nevertheless, maybe the debugging procedure below will be helpful ...)

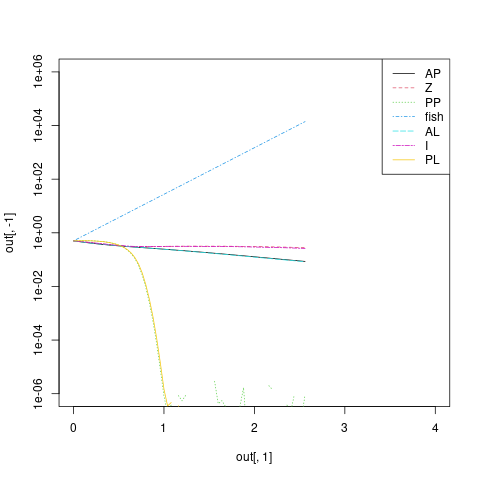
I ran the model with a much smaller delta-t over a smaller time horizon to try to see which state variables were problematic.

out <- ode(yini, seq(0, 4, length.out = 101), vade_2005_model, pars, method = "ode45")
matplot(out[,1], out[,-1], type = "l", log = "y", ylim = c(1e-6, 1e6),
        lty = 1:7, col = 1:7)
legend("topright",
       legend = colnames(out)[-1],
       col = 1:7,
       lty = 1:7)

It looks like the fish population is exploding and the PP/PL populations are crashing (which would follow naturally from an exploding fish population; in principle if the equations are well-posed this wouldn't lead to a mathematical problem, but it's not surprising that this is causing numerical problems).

Went back and looked at the dF/dt equation, and sure enough, found the typo.

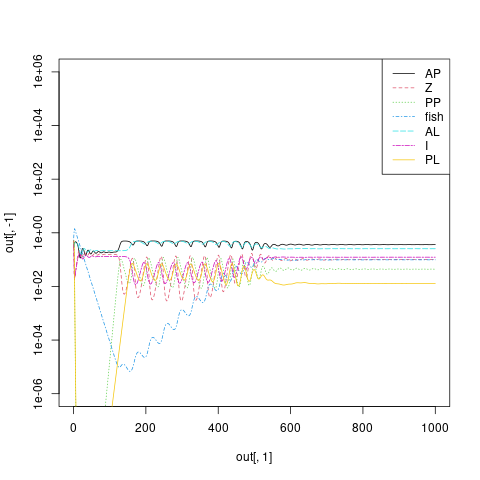
Re-running from 0 to 1000 with the corrected denominators: