I recently did an experiment where I measured the output signal of an RLC circuit which behaves exactly like a damped free harmonic oscillator. I want to to dermine the damping ratio from the data. My first idea was to use a decaying exponential fit on the enveloppe, as depicted in the following Figure.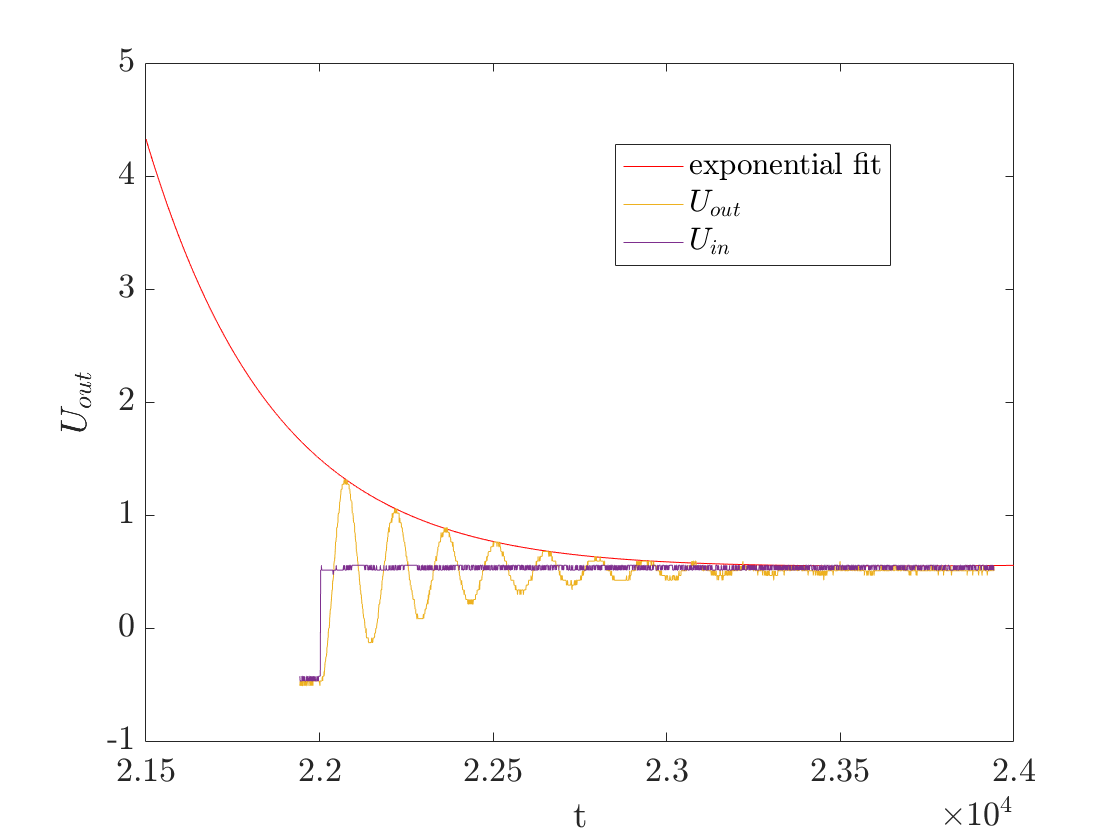

After many hours of despair, I managed to use the Curve Fitting tool provided by Matlab to add an exponential fit, but I had to select manually the peaks to take into account. Is there any way to achieve this same result but with code ?

I mean, I know there has to be a way, but I've been struggling for more time than should be legally permitted, so If any kind soul could help me with a script, I'd warmheartedly welcome it. I can use either Gnuplot, python or Matlab.

Thanks in advance

Here is a link to the full data file, since SO doesn't let me dump the whole content here

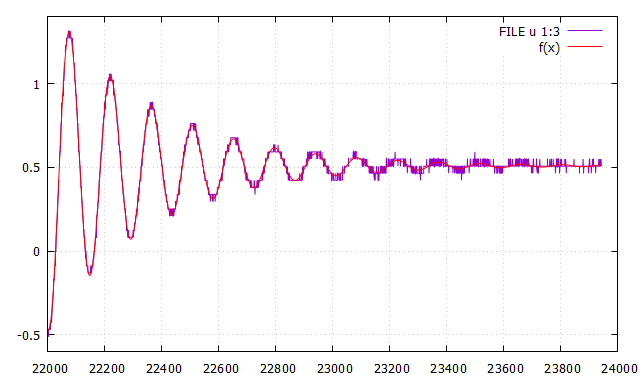
CodePudding user response：

The exponential model approach looks reasonable to me. If you have an algorithm to find the peaks automatically you can put those into your exponential decay model without having manually select them. There are multiple ways to do this and I have had to "solve" this problem different ways depending on the complexity (noise, periodicity, etc.) of the input data. If your signal is pretty clean I would go with the following approach.

Vi = V - mean(V);   %remove the mean of the signal
[OPTIONAL]...Vi = filter(B,1,Vi);  %apply low pass filter (B) 
[Pks,Locs] = findpeaks(Vi,'MinPeakDistance',D) %assuming you have an estimate of the frequency, set the value of D to something like 75% of the expected period so that you only detect peaks that are separated by the expected amount

At this point, you could do some further checks on the Pks and Locs to qualify them, but otherwise these are the inputs to your exponential model.