Matplotlib hist doesn't calculate the correct heights of bars-CodePudding

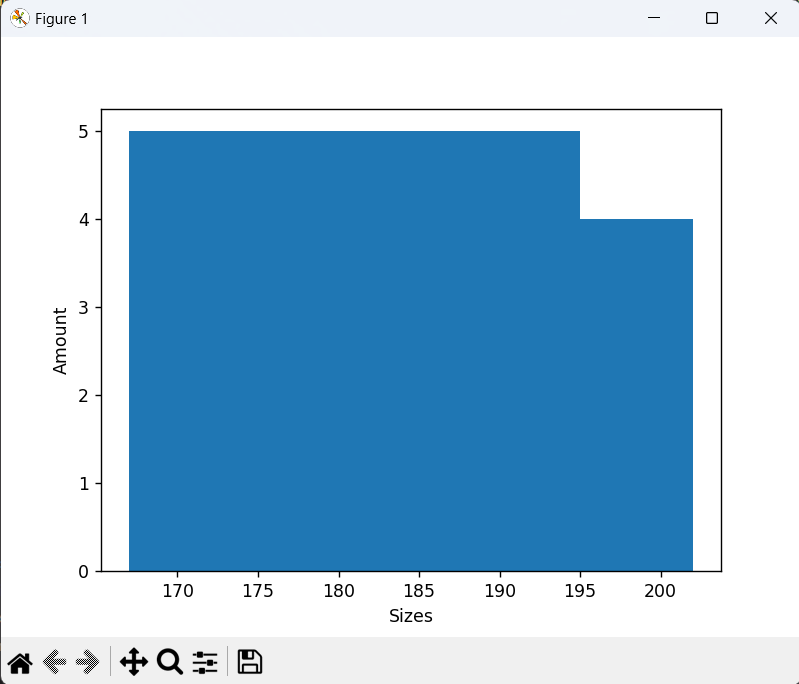
I read data from a csv file and then calculate the amount of bins according to sturges rule. Then I make a histogram using matplotlib, but I don't get what I expect.

import matplotlib.pyplot as plot

height = [167, 170, 173, 173, 173, 174, 175, 178, 180, 180, 182, 182, 184, 185, 187, 188, 189, 190, 192, 193, 195, 197, 199, 202]
plot.hist(height, bins=5)
plot.xlabel("Sizes")
plot.ylabel("Count")
plot.show()

Which gets me the following output:

But I would expect the counts in the different ranges to be:

167 - 174.0: 6
174.0 - 181.0: 4
181.0 - 188.0: 6
188.0 - 195.0: 5
195.0 - 202.0: 3

What can I do to fix the plot or am I thinking about this wrong?

CodePudding user response：

Here is a text version of what you graphically depicted.

>>> hst = plot.hist(height, bins=5)
>>> for patch in hst[2].patches:
...     print(patch.get_bbox())
... 
Bbox(x0=167.0, y0=0.0, x1=174.0, y1=5.0)
Bbox(x0=174.0, y0=0.0, x1=181.0, y1=5.0)
Bbox(x0=181.0, y0=0.0, x1=188.0, y1=5.0)
Bbox(x0=188.0, y0=0.0, x1=195.0, y1=5.0)
Bbox(x0=195.0, y0=0.0, x1=202.0, y1=4.0)

Input points (heights) belong to exactly one bin. Each bin is a half-open interval, similar to what range() uses. The first couple of bins are:

167 <= height < 174
174 <= height < 181
...

The final bin is a minor exception to that rule:

195 <= height <= 202

Apparently you want some of these input points to appear in neighboring bins. Consider defining some small epsilon value:

    eps = 1e-3

and then add or subtract that from selected data points to acheive the desired result.

Notice that adjusting the initial (167) value by epsilon will adjust the start of all bins, possibly giving you what you were looking for. And similarly for the final (202) value.

Let's assume these are height measurements in cm for some population of individuals, and that the measurement technique is precise to roughly a millimeter. That might correspond to this (non-deterministic!) situation:

import numpy as np

eps = .1
height = np.array(height)   np.random.normal(scale=eps, size=len(height))

(Use list( ... ) on that if you prefer not to work with a numpy array.)

Each time you plot such values you will obtain a slightly different graphical depiction. They will be plausibly consistent with small real-world measurement errors.