#include<conio.h>
#include<math.h>
int sum(int n);
int main()
{
printf("sum is %d", sum(5));
return 0;
}
//recursive function
int sum(int n)
{
if(n==1)
{
return 1;
}
int sumNm1=sum(n-1); //sum of 1 to n
int sumN=sumNm1 n;
}
Here i didn't understand how this code works when n==1 becomes true, How this code backtracks itself afterwards..?
CodePudding user response:
The code needs a return statement in the case where n is not 1:
int sum(int n)
{
if(n==1)
{
return 1;
}
int sumNm1=sum(n-1); //sum of 1 to n
int sumN=sumNm1 n;
return sumN;
}
or more simply:
int sum(int n)
{
if(n==1)
{
return 1;
}
return n sum(n-1);
}
How this code backtracks itself afterwards..?
When a function is called, the program saves information about hwo to get back to the calling context. When return statement is executed, the program uses the saved information to return to the calling context.
This is usually implemented via a hardware stack, a region of memory set aside for this purpose. There is a stack pointer that points to the active portion of the stack memory. When main calls sum(5), a return address into main is pushed onto the stack, and the stack pointer is adjusted to point to memory that is then used for the local variables in sum. When sum calls sum(n-1), which is sum(4), a return address into sum is pushed onto the stack, and the stack pointer is adjusted again. This continues for sum(3), sum(2), and sum(1). For sum(1), the function returns 1, and the saved return address is used to go back to the previous execution of sum, for sum(2), and the stack pointer is adjusted in the reverse direction. Then the returned value 1 is added to its n, and 3 is returned. The saved address is used to go back to the previous execution, and the stack pointer is again adjusted in the reverse direction. This continues until the original sum(5) is executing again. It returns 15 and uses the saved address to go back to main.
CodePudding user response:
When n is 1, the function returns 1. When n is 2, the function calls itself for n is 1, so it gets 1, and then adds n (i.e., 2) to it. When n is 3, the function calls itself for n is 2, so it gets 3, and then adds n (i.e., 3) to it. And so on.
CodePudding user response:
How this code backtracks itself afterwards..?
It doesn't certainly work.
Any success is due to undefined behavior (UB).
The biggest mistake is not compiling with a well enabled compiler.
int sum(int n)
{
if(n==1)
{
return 1;
}
int sumNm1=sum(n-1); //sum of 1 to n
int sumN=sumNm1 n; // !! What, no warning?
} // !! What, no warning?
A well enabled compiler generates warnings something like the below.
warning: unused variable 'sumN' [-Wunused-variable]
warning: control reaches end of non-void function [-Wreturn-type]
Save time and enable all compiler warnings. You get faster feedback to code troubles than posting on SO.
int sumN=sumNm1 n;
return sumN; // Add
}
CodePudding user response:
Like pointed in comments, the problem is that you don't return the value you compute from within the function (Undefined Behavior). You calculate it correctly (but in a clumsy way, using 2 unneeded variables). If you add a return sumN; statement at the end of the function, things should be fine.
Also, the type chosen for the return value is not the best one. You should choose:
An unsigned type (as we are talking about natural numbers), otherwise half of its interval would be simply wasted (on negative values which won't be used)
One that's as large as possible (uint64_t). Note that this only allows larger values to be computed, but does not eliminate the possibility of an overflow, so you should also be careful when choosing the input type (uint32_t)
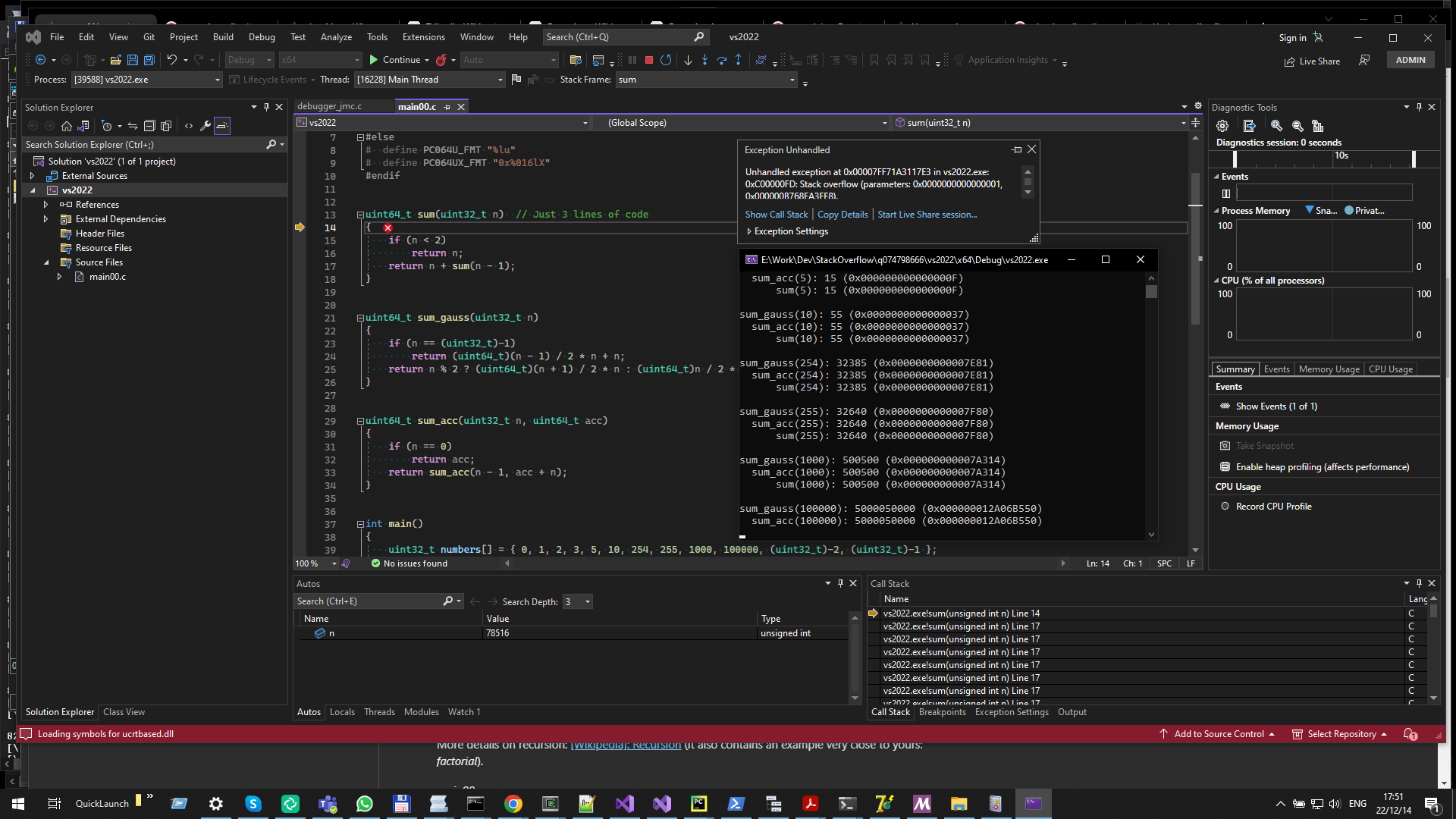
As seen in the image above, the simple implementation (sum) failed while the other 2 passed (for a certain (big) input value). Not sure though why it didn't also fail on Linux (WSL), most likely one of the optimizations (from -O2) enabled tail-end-recursion (or increased the stack?).
CodePudding user response:
If I understand your question correctly, you're more interested in how recursion actually works, than in the error produced by the missing return statement (see any of the other answers).
So here's my personal guide to understanding recurive functions.
If you know about Mathematical Induction, this might help understand how recursion works (a least it did for me). You prove a base case(, make an assumption about a fixed value) and prove the statement for a following number. In programming we do a very similar thing.
Firstly, identify your base cases, i.e. some input to the function that you know what the output is. In your example this is
if(n==1)
{
return 1;
}
Now, we need to find a way to compute the value for any given input from "smaller" inputs; in this case sum(n) = sum(n-1) n.
How does backtracking work after the base case has been reached?
To understand this, picture the function call sum(2).
We first find that 2 does not match our base case, so we recursively call the function with sum(2-1). You can imagine this recursive call as the function called with sum(2) halting until sum(1) has returned a result. Now sum(1) is the "active" function, and we find that it matches our base case, so we return 1. This is now returned to where sum(2) has waited for the result, and this function now can compute 2 sum(1), because we got the result from the recursive call.
This goes on like this for every recursive call, that is made.
Interested in a bit more low-level explanation?
In assembly (MIPS), your code would look something like this:
sum:
addi $t1, $0, 1 # store '1' in $t0
beq $a0, $t0, base # IF n == 1: GOTO base
# ELSE:
# prepare for recursive call:
sw $a0, 4($sp) # write n on top of the stack
sw %ra, 8($sp) # write the line of the caller on top of stack
addi $sp, $sp, 8 # advance stack pointer
addi $a0, $a0, -1 # n = n-1
jal sum # call sum with reduced n
# this is executed AFTER the recursive call
addi $sp, $sp, -8 # reset stack pointer
lw %ra, 8($sp) # load where to exit the function
lw