I got assigned to solve this problem: Given number of products sold in specific stores, is there a way to find from which stores to buy all products with the condition of buying only one product from each store.

For example if you have stores A,B,C and products a,b,c with each shop selling:

A: a,c

B: a,b,c

C: c

Answer: You will be buying products a from store A product b from store B and product c from store C.

From this am assuming you cant have more products than stores since you are buying just 1 product from each store and you want to buy all of them.

My thought was using a greedy algorithm where you first buy products exclusively sold in one store and solving this hierarchically but it doesn't always work

CodePudding user response：

You could solve it by finding the max-flow on a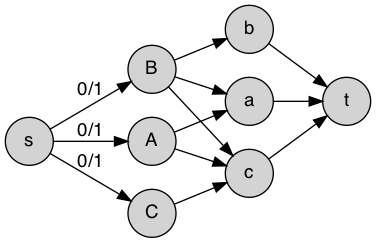

Then apply the greedy Ford–Fulkerson method. If the max-flow reaches the number of stores and the number of products, then one has a viable solution.

CodePudding user response：

it took me a while but i created some c# with my approach to the problem:

class BuyFromShops
{
    private static Dictionary<string, List<string>> _shops = new()
    {
        { "A", new List<string> { "a", "b" } },
        { "B", new List<string> { "a", "b", "c" } },
        { "C", new List<string> { "c" } }
    };

    static void Main(string[] args)
    {
        // the items that have been bought
        var itemsBought = new List<string>();

        // sort items by how often they are sold
        List<string> itemsToBuy = GetDistinctItemsSortedByCountAscending();

        // sort shops by amount of items
        List<string> shopsToBuyFrom = GetShopSortedByItemCountDescending();

        // for shop from most items to least
        foreach (var shop in shopsToBuyFrom)
        {
            // for items from rarest to most common
            foreach (var item in itemsToBuy)
            {
                // if item is in shop remove item and go to next store
                string baughtItem = string.Empty;
                if (_shops[shop].Contains(item) && !itemsBought.Contains(item))
                {
                    _shops[shop].Remove(item);
                    itemsBought.Add(item);
                    baughtItem = item;
                    Console.WriteLine($"Bought {item} from {shop}.");
                }

                if (baughtItem == string.Empty) continue;
                itemsToBuy.Remove(baughtItem);
                break;
            }
        }

        Console.WriteLine("Remaining items in shops.");
        foreach (var shop in _shops)
        {
            Console.WriteLine($"{shop.Key}: {string.Join(", ", shop.Value)}");
        }

        Console.WriteLine($"Items bought: {string.Join(", ", itemsBought)}");
    }

    private static List<string> GetShopSortedByItemCountDescending()
    {
        var result = from entry in _shops orderby entry.Value.Count descending select entry.Key;
        return result.ToList();
    }

    private static void BuyItem(string store, string item)
    {
        _shops[store].Remove(item);
    }

    private static List<string> GetDistinctItemsSortedByCountAscending()
    {
        var distinctItems = new Dictionary<string, int>();

        foreach (string item in _shops.SelectMany(shop => shop.Value))
        {
            if (!distinctItems.ContainsKey(item))
            {
                distinctItems.Add(item, 1);
            }
            else
            {
                distinctItems[item]  = 1;
            }
        }

        var distinctItemsSorted = from entry in distinctItems orderby entry.Value select entry.Key;
        return distinctItemsSorted.ToList();
    }
}

CodePudding user response：

My Python code, prints the solution:

stores = ['A', 'B', 'C']
products = ['a', 'b', 'c']

# Initialize the product inventory in each store
# A: a,c
# B: a,b,c
# C: c
inventory = {
    'A': ['a', 'c'], 
    'B': ['a', 'b', 'c'], 
    'C': ['c']
}

# Greedy algorithm to allocate products to stores
allocated_products = {}
for product in products:
    allocated_products[product] = None

for store in stores:
    for product in inventory[store]:
        if allocated_products[product] == None:
            allocated_products[product] = store
            break

# Print the solution
for product, store in allocated_products.items():
    print(f'Product: {product}, Store: {store}')