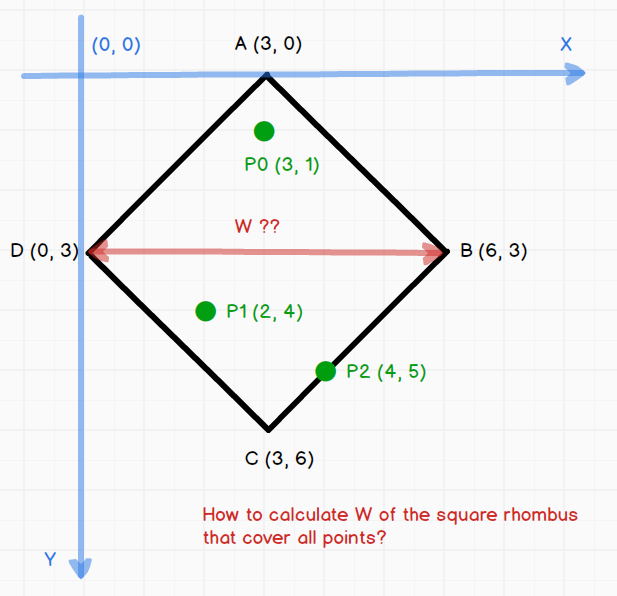
How to calculate width of the square rhombus that cover all points?
We know only points, and need to find W. There can be any number of points.

Example 1

Example 2

CodePudding user response：

You can look at an equivalent problem where you

1. Rotate all the points by 45 degrees
2. Shift them such that all the points have non-negative X and Y coordinates.
3. At least 1 point in the set has '0' X coordinate
4. At least 1 point in the set has '0' Y coordinate

Try to find a square which is parallel to the X axis and the Y axis which covers all the points. Such a square will be the square with a diagonal from the origin towards the largest X coordinate, noted as x_max, and the largest Y coordinate, noted as 'y_max', from the point set (not necessarily from the same point).

Thuerefore, W will take the the form of:

W = sqrt(x_max ** 2   y_max ** 2)

Which is the 2-norm of the coordinate in the far-end of the diagonal (x_max, y_max)

CodePudding user response：

Rotate all point coordinates by Pi/4 (45 degrees) relative to coordinate origin, and find minimum and maximum values for both X and Y coordinates. Maximal difference from xmax-xmin, ymax-xmin is square side size.

CodePudding user response：

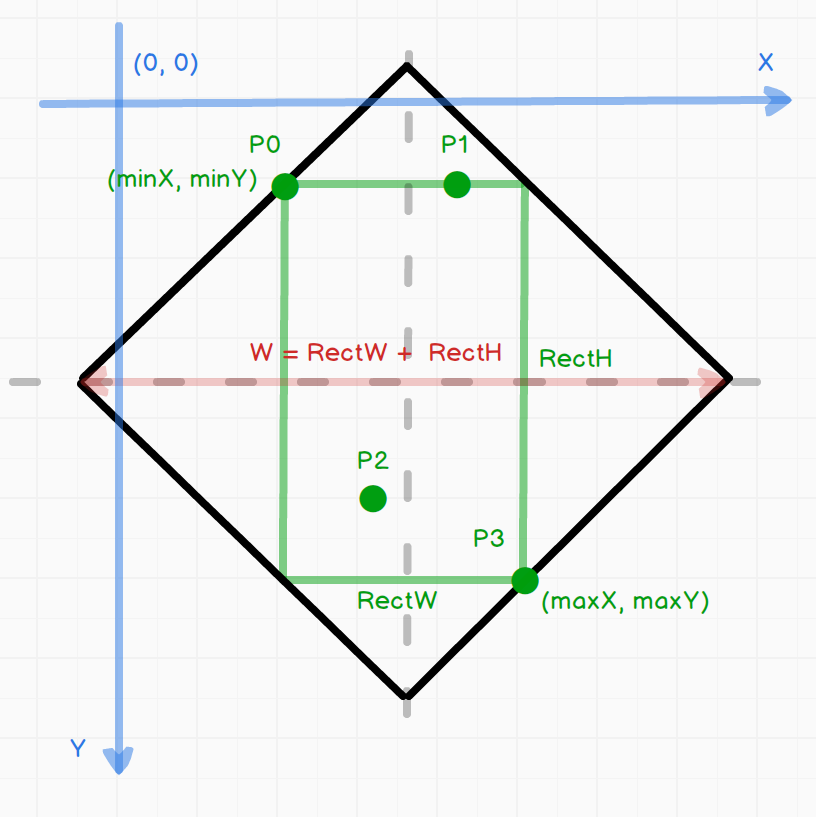
I think I found solution without rotation all the points by 45 degrees.

1. Get rectangle that cover all points.
   To do that find (minX, minY) and (maxX, maxY) points
2. There is only one way to place rectangle in a square rhombus - see img
   Based on a img: W = RectW RectH

CodePudding user response：

1. create 2 basis vectors u,v for your rhombus

   float c = sqrt(0.5) = 0.70710678118654752440084436210485
   vec2 u = vec2( c, c)
   vec2 v = vec2( c,-c)
   

2. find BBOX using u,v

   float u0 = min(dot(u,p[i]))
   float u1 = max(dot(u,p[i]))
   float v0 = min(dot(v,p[i]))
   float v1 = max(dot(v,p[i]))
   

   where vec3 p[] are your points

3. construct rhombus points

   vec2 p0 = u0*u   v0*v
   vec2 p1 = u1*u   v0*v
   vec2 p2 = u1*u   v1*v
   vec2 p3 = u0*u   v1*v
   

In case you are not familiar with vector math dot(a,b) in 2D is:

dot(a,b) = (a.x*b.x)   (a.y*b.y)