I was solving a Leetcode's 77 called "Combinations". Here's the problem statement:

Given two integers n and k, return all possible combinations of k numbers chosen from the range [1,n]. You may return the answer in any order.

And here's my code:

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        return combine(1, new LinkedList<>(), k, new ArrayList<>(), n);
    }

    private List<List<Integer>> combine(int start, LinkedList<Integer> comb, int k, List<List<Integer>> result, int n){
        if(k == 0){
            result.add(new LinkedList<>(comb));
            return result;
        }

        for(int i = start; i <= n-k 1; i  ){
            comb.add(i);
            combine(i 1, comb, k-1, result, n);
            comb.pollLast();
        }
        return result;
    }
}

Although this code was working perfectly fine, but I'm stuck on evaluating the Time and Space complexity for this algorithm.

What would be the Time and Space complexity of the solution presented above?

CodePudding user response：

The time complexity of the presented solution is O(k * n! / (k! * (n-k)!)).

Because the time complexity for this task is naturally bounded by the number of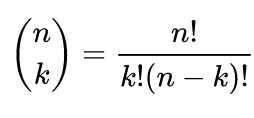

And for each generated combination, we need to construct a new List of size k, all other costs are constant.

Therefore, the resulting time complexity would be O(k * ( n!/(k!*(n-k)!)).

And since we need to allocate in memory all n!/(k!*(n-k)!) combinations each of size k, and there's no additional space required by the algorithm apart from that, space complexity would be also O(k * ( n!/(k!*(n-k)!)).