How to find a x-value for a known y-value on a titration curve graph in python?-CodePudding

I have a graph in python (not a graph made by arrays) and now I need to find the x-value for y=7.

This is my code:

from pHcalc.pHcalc import Acid, Neutral, System
import numpy as np
import matplotlib.pyplot as plt 

# Phosphoric acid
# Define acid solution 
start_vol = 0.010 # liter
conc_acid=0.5 # mol/liter, starting concentration
Ka_acid=[7.11E-003, 6.34E-008, 4.22E-013]
charge_acid=0 

# Define titrant
conc_base=1.0 # mol/liter, starting concentration
max_vol_titrant=0.007 # Liter
charge_base=1 # 1 for NaOH

#Compute pHs for different titrant volumes and plot
phs = []
titrant_vols = np.linspace(0,max_vol_titrant,200)
for tvol in titrant_vols:
    acid = Acid(Ka=Ka_acid, charge=charge_acid, conc=conc_acid*start_vol/(start_vol tvol)) #weak acid
    base = Neutral(charge=charge_base, conc=conc_base*tvol/(start_vol tvol)) #strong base
    system = System(acid, base)
    system.pHsolve(guess_est=True)
    phs.append(system.pH)
plt.plot(titrant_vols*1000, phs)
plt.ylabel('pH')
plt.xlabel('ml titrant')
plt.show()

I searched a lot online but cannot find anywhere a function that will give me the x-value for a given x-value.

CodePudding user response：

That is not a matplotlib job. Matplotlib job is to draw things. I get that, from a human point of view, one way to figure that out is from drawing, but drawing is just a way to present data, that you already have.

I would use interpolation for such a task

import scipy.interpolate
# Once you've computed phs and titrant_vols, you can compute an interpolation
# function that can guess one from the other
volFromPh=scipy.interpolate.interp1d(phs,titrant_vols, fill_value='extrapolate')
# Then call volFromPh from any data (or array of datas)
volFromPh(5)
# → 0.00502533 (5.03 ml)

# Graphical verification (after all, since we have matplotlib, even if your
# question is not related to it, now that it is here...)
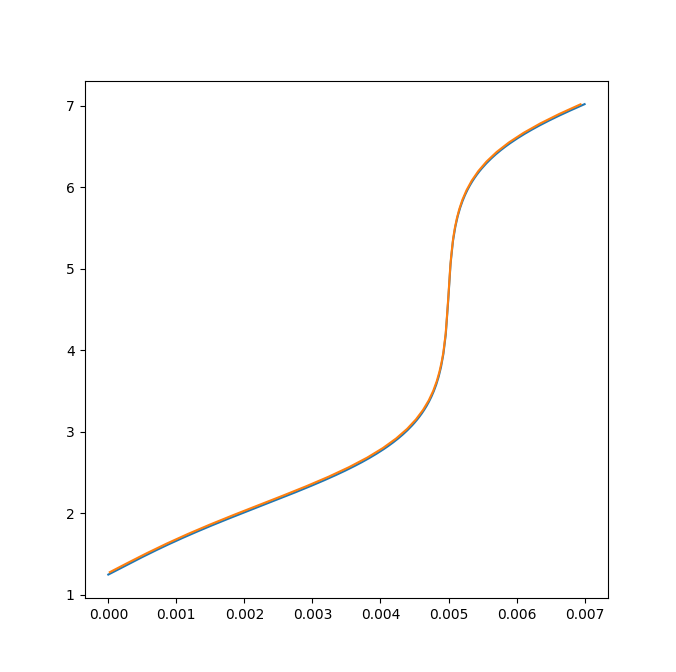
simPh=np.linspace(1.26,7,50) 
simVol=volFromPh(simPh)
plt.plot(simVol, simPh 0.02) #  0.02 is so that we can tell the 2 curve from each other
plt.plot(titrant_vols, phs)

You can see that the curve made of "y" you computed from "x" is almost exactly superposed with the one made of "x" computed from "y" (from interpolation from the previous x,y). If it were not for the 0.02, we could not see that there are 2 curves.

So, solution is unrelated to plotting (even if I use plot to demonstrate it). Just use the dataset of x,y to create a function with scipy.interpolate to estimate x from y.