simulating an observational dataset for a teaching example-CodePudding

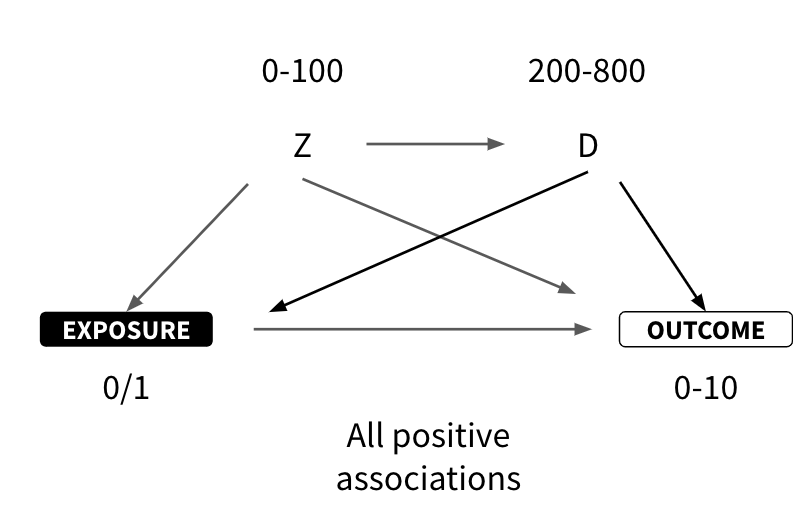
I'm looking for help simulating an observational dataset in R where the correlated variables Z and D confound the relationship between the exposure (0/1) and the outcome (0-10).

This

CodePudding user response：

How about something like this:

set.seed(123)
b <- replicate(2500, {
  Z <- runif(250, 0, 100)
  D <- scales::rescale(Z   rnorm(250, 0, 20), to=c(200, 800))
  q_esposure <- -5   (1/sd(Z))*Z   (1/sd(D))*D
  exposure <- rbinom(250, 1, plogis(q_esposure))
  error <- rnorm(250, 0, 1)
  outcome <-  error   .01*D   .1*Z
  outcome <- scales::rescale(outcome, to=c(0, 8.5))
  outcome <- outcome   1.5*exposure
  lm(outcome ~ Z   D   exposure)$coef
})

rowMeans(b)
#>  (Intercept)            Z            D     exposure 
#> -0.722225550  0.049755855  0.004978287  1.500040770

^{Created on 2022-12-31 by the reprex package (v2.0.1)}

CodePudding user response：

If you are looking for a single data set with the specified characteristics, you could try:

set.seed(4410)

Z        <- sample(100, 1000, TRUE)
D        <- Z   rnorm(1000, 0, 20)
D        <- round((D - min(D)) / diff(range(D)) * 600   200)
Exposure <- rbinom(1000, 1, (D   Z) / 1000)
Outcome  <-  rbinom(1000, 10,  (Exposure   2.3) / 6.6   (D   Z)/2000)

df <- data.frame(Exposure, Outcome, Z, D)

Note that this gives all integers, and each of the integers is within the specified range for each variable:

head(df)
#>   Exposure Outcome  Z   D
#> 1        0       4  8 344
#> 2        0       5 15 372
#> 3        1       7 39 549
#> 4        0       6 66 508
#> 5        1       9 78 570
#> 6        1       9 28 347

lapply(df, range)
#> $Exposure
#> [1] 0 1
#> 
#> $Outcome
#> [1]  1 10
#> 
#> $Z
#> [1]   1 100
#> 
#> $D
#> [1] 200 800

We can confirm that Z and D are positively correlated with each other, and that both Z and D are positively correlated with Exposure:

cor(df$Z, df$D)
#> [1] 0.832381
cor(df$Z, df$Exposure)
#> [1] 0.235582
cor(df$D, df$Exposure)
#> [1] 0.2367981

Without taking the confounders into account, the effect of Exposure is about 1.8:

lm(Outcome ~ Exposure, data = df)
#> 
#> Call:
#> lm(formula = Outcome ~ Exposure, data = df)
#> 
#> Coefficients:
#> (Intercept)     Exposure  
#>       6.127        1.795

But taking the confounders into account, we can see that the coefficient for Exposure is 1.5

summary(lm(Outcome ~ Exposure   Z   D, data = df))
#> 
#> Call:
#> lm(formula = Outcome ~ Exposure   Z   D, data = df)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -4.5112 -0.9401  0.0876  0.9671  4.1952 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 3.8034249  0.2496879  15.233  < 2e-16 ***
#> Exposure    1.5000019  0.0900666  16.654  < 2e-16 ***
#> Z           0.0035773  0.0027056   1.322    0.186    
#> D           0.0045452  0.0006929   6.560 8.65e-11 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 1.364 on 996 degrees of freedom
#> Multiple R-squared:  0.378,  Adjusted R-squared:  0.3761 
#> F-statistic: 201.7 on 3 and 996 DF,  p-value: < 2.2e-16

^{Created on 2022-12-31 with reprex v2.0.2}