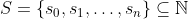I have a zero-initialized boolean array of size N, and a set of distinct positive integers S.

For each element in S denoted as e, I would like to set every element whose 1-indexed number is divisible by e to true.

For example, given N=6 and S={2, 3}, the resulting array would be {0, 1, 1, 1, 0, 1}.

A simple implementation of this in C would look like this:

bool arr[N]{};
for(int e : S) {
    for(int i = e-1; i < N; i  = e) {
        arr[i] = true;
    }
}

This works just fine, however, it is not fast enough. Given that S could have up to N elements, this results in a quadratic time complexity O(N^2).

Note that I only need to calculate the number of elements in the array that are set to true in the end.

So I was wondering, is there a faster way to approach this since I only need to know the number of true values in the array afterwards?

Preferably in a time complexity of O(NlogN) or better.

CodePudding user response：

First off, your complexity is in no way O(N²), since the cardinality of S is not strictly linked to that of N, we can say that your program runs in O(N*k) where k = |S|.

For k << N, there might be a solution that is faster...

The theory

that is, given a set of numbers:

We can construct a sequence of their multiples M, and we are also assured that M is going to repeat exactly after 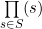times, that is, after we compute this sequence up to the number obtained by multiplying all members of s, we can tile it infinitely, we are going to call this special number L.

This, in turn, means that if we have a producer of such a sequence (which still requires to perform the above algorithm for the first L numbers), we can then use the resulting sequence to randomly access our array and set the bits to true, thus amortizing the costs

A possible implementation

First off, we can define a function to generate this sequence M, then another to properly fill the array given this sequence, we call both and then print the result to stdout:

#include <iostream>
#include <iterator>
#include <ranges>
#include <numeric>
#include <algorithm>
#include <vector>
#include <concepts>

#define N 6


[[nodiscard]] constexpr std::vector<int> MultiplesSequence(std::ranges::range auto const& range, int max_size) noexcept {  
        
        int max = std::accumulate(range.begin(), range.end(), 1, std::multiplies<int>());
        // avoid calculating multiples if the don't correspond to indices in the array
        max = std::min(max, max_size);

        std::vector<int> multiples;
        for(auto n : std::ranges::views::iota(1, max)) {
            if(std::ranges::any_of(range, [n](auto&& i) { return n % i == 0; })) {
                multiples.push_back(n);
            }
        }

        return multiples;
    }

constexpr void fill_bool(auto& bool_arr, auto const& multiples)
{
    // we might have optimized all multiples out
    if(multiples.empty()) {
        return;
    }
    // not the most elegant solution for wraparound
    auto highest = multiples.back();
    auto times = 1   N  / highest;

    for(int n = 1; n <= times;   n) {
        for(auto m : multiples) {
            if(n * m <= N)
            {
                bool_arr[n * m - 1] = true;
            }
        }
    }
}

int main()
{
    bool arr[N]{};
    std::vector<int> S = {2, 3};
    auto multiples = MultiplesSequence(S, N);
    fill_bool(arr, multiples);

    std::copy(arr, arr   N, std::ostream_iterator<bool>(std::cout, " "));

}

In general, a person more proficient with the language might come up with an implementation based on std::unreachable_sentinel to properly simulate an infinite sequence and then take from it from a view adaptor, in a similar way as what is shown in this solution, this gets the job done anyway.

This way, we pay an O(L*k) cost (we find the multiples only up to the special length L) and then we can quickly insert the rest in linear time, how much this is worth in practice warrants profiling.

CodePudding user response：

A simple optimization improves things quite a bit if members of S can be multiples of other members of S

bool arr[N]{};
for(int e : S) {
    if (arr[e-1] != true) {
        for(int i = e-1; i < N; i  = e) {
            arr[i] = true;
        }
    }
}

The idea being that if arr[e-1] has already been set, then all of its multiples have been, as well.