I am now using lists to represent the graph, which would be similar to 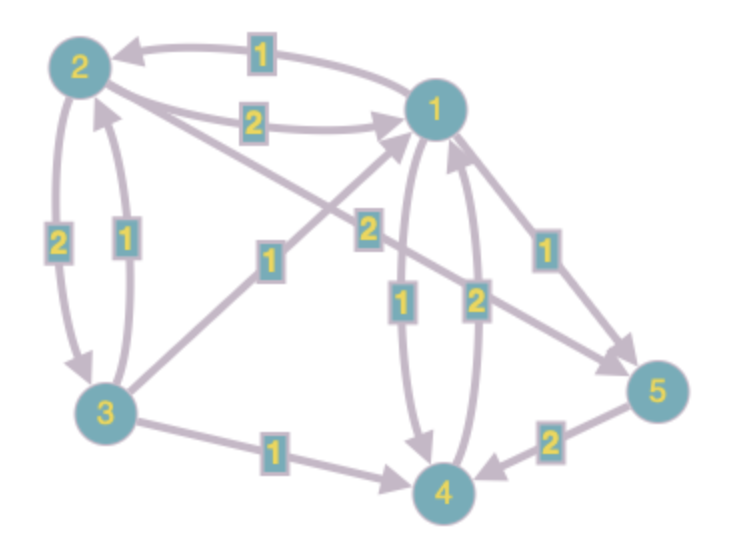
is now represented as:
nodes = ["1", "2", "3", "4", "5"]
edges = [
[0, 2, 1, 2, 0],
[1, 0, 1, 0, 0],
[0, 2, 0, 0, 0],
[1, 0, 1, 0, 2],
[1, 2, 0, 0, 0],
]
Here, edge weights can only be 1 or 2 and 0 represents no edge from one node to other. The edges are directed, so every list in the matrix represents the edges coming toward the node.
Similar to the last question, I want all possible two-edge modifications on the graph. So, for example, if we add an edge from node "4" to "5" with weight of 1, and remove the edge with weight 1 coming from node "1" to "4", the new graph will look like:
edges = [
[0, 2, 1, 2, 0],
[1, 0, 1, 0, 0],
[0, 2, 0, 0, 0],
[0, 0, 1, 0, 2],
[1, 2, 0, 1, 0],
]
and this is one of the possible modifications.
I want to build a generator that can create all such modifications sequentially and pass it to me so that I can use them to test.
My code so far is like this:
def all_modification_generation(graph: list[list], iter_count: int = 0):
possible_weights = {-1, 0, 1}
node_len = len(graph)
for i in range(node_len**2):
ix_x = i // node_len
ix_y = i % node_len
if i == ix_y:
continue
for possible_pertubs in possible_weights - {graph[ix_x][ix_y]}:
graph[ix_x][ix_y] = possible_pertubs
if iter_count == 0:
all_modification_generation(graph=graph, iter_count=iter_count 1)
else:
yield all_modification_generation(graph=graph)
My logic is, once I do one change, I can then loop over all other elements that come after it in the matrix. So this problem could be solved recursively. And once a node is explored, we do not need to take it into consideration for next loops, because it will just give us a duplicate result that we have already found. And because I need to check for 2 modifications, I am increasing iter_count after first iteration and then yielding the next time. I am skipping ix_x == ix_y cases because a self-looping edge does not make any sense in this context, so that change is not required to be recorded.
But even then, this does not output any result. What am I doing wrong? Any help is appreciated, thanks!
Edit: I think I have figured out a way to do the double modification without repetitive generation of modified matrices. Now the only problem is that there is quite a bit of code repetition and a 4-level nested for-loop.
I'm not sure how to call a generator recursively, but I feel that should be the way to go! Thanks J_H for pointing me to the right direction.
The working code is:
def all_modification_generation(graph: list[list]):
possible_weights = {-1, 0, 1}
node_len = len(graph)
for i in range(node_len**2):
ix_x1 = i // node_len
ix_y1 = i % node_len
if ix_x1 == ix_y1:
continue
for possible_pertubs in possible_weights - {graph[ix_x1][ix_y1]}:
cc1_graph = deepcopy(graph)
cc1_graph[ix_x1][ix_y1] = possible_pertubs
for j in range(i 1, node_len**2):
ix_x2 = j // node_len
ix_y2 = j % node_len
if ix_x2 == ix_y2:
continue
for possible_perturbs2 in possible_weights - {cc1_graph[ix_x2][ix_y2]}:
cc2_graph = deepcopy(cc1_graph)
cc2_graph[ix_x2][ix_y2] = possible_perturbs2
yield cc2_graph
CodePudding user response:
The quadratic looping is an interesting technique.
We do wind up with quite a few repeated
division results, from // node_len, but that's fine.
I had a "base edits" datastructure in mind for this problem.
Converting array to list-of-lists would be straightforward.
After overhead, a 5-node graph consumes 25 bytes -- pretty compact. Numpy offers good support for several styles of sparse graphs, should that become of interest.
from typing import Generator, Optional
import numpy as np
class GraphEdit:
"""A digraph with many base edge weights plus a handful of edited weights."""
def __init__(self, edge: np.ndarray, edit: Optional[dict] = None):
a, b = edge.shape
assert a == b, f"Expected square matrix, got {a}x{b}"
self.edge = edge # We treat these as immutable weights.
self.edit = edit or {}
@property
def num_nodes(self):
return len(self.edge)
def __getitem__(self, item):
return self.edit.get(item, self.edge[item])
def __setitem__(self, item, value):
self.edit[item] = value
def as_array(g: GraphEdit) -> np.ndarray:
return np.array([[g[i, j] for j in range(g.num_nodes)] for i in range(g.num_nodes)])
def all_single_mods(g: GraphEdit) -> Generator[GraphEdit, None, None]:
"""Generates all possible single-edge modifications to the graph."""
orig_edit = g.edit.copy()
for i in range(g.num_nodes):
for j in range(g.num_nodes):
if i == j: # not an edge -- we don't support self-loops
continue
valid_weights = {0, 1, 2} - {g[i, j]}
for w in sorted(valid_weights):
yield GraphEdit(g.edge, {**orig_edit, (i, j): w})
def all_mods(g: GraphEdit, depth: int) -> Generator[GraphEdit, None, None]:
assert depth >= 1
if depth == 1:
yield from all_single_mods(g)
else:
for gm in all_single_mods(g):
yield from all_mods(gm, depth - 1)
def all_double_mods(g: GraphEdit) -> Generator[GraphEdit, None, None]:
"""Generates all possible double-edge modifications to the graph."""
yield from all_mods(g, 2)
Here's the associated test suite.
import unittest
from numpy.testing import assert_array_equal
import numpy as np
from .graph_edit import GraphEdit, all_double_mods, all_single_mods, as_array
class GraphEditTest(unittest.TestCase):
def setUp(self):
self.g = GraphEdit(
np.array(
[
[0, 2, 1, 2, 0],
[1, 0, 1, 0, 0],
[0, 2, 0, 0, 0],
[1, 0, 1, 0, 2],
[1, 2, 0, 0, 0],
],
dtype=np.uint8,
)
)
def test_graph_edit(self):
g = self.g
self.assertEqual(5, self.g.num_nodes)
self.assertEqual(2, g[0, 1])
g[0, 1] = 3
self.assertEqual(3, g[0, 1])
del g.edit[(0, 1)]
self.assertEqual(2, g[0, 1])
def test_non_square(self):
with self.assertRaises(AssertionError):
GraphEdit(np.array([[0, 0], [1, 1], [2, 2]]))
def test_all_single_mods(self):
g = GraphEdit(np.array([[0, 0], [1, 0]]))
self.assertEqual(4, len(list(all_single_mods(g))))
expected = [
np.array([[0, 1], [1, 0]]),
np.array([[0, 2], [1, 0]]),
np.array([[0, 0], [0, 0]]),
np.array([[0, 0], [2, 0]]),
]
for ex, actual in zip(
expected,
map(as_array, all_single_mods(g)),
):
assert_array_equal(ex, actual)
# Now verify that original graph is untouched.
assert_array_equal(
np.array([[0, 0], [1, 0]]),
as_array(g),
)
def test_all_double_mods(self):
g = GraphEdit(np.array([[0, 0], [1, 0]]))
self.assertEqual(16, len(list(all_double_mods(g))))
expected = [
np.array([[0, 0], [1, 0]]),
np.array([[0, 2], [1, 0]]),
np.array([[0, 1], [0, 0]]),
np.array([[0, 1], [2, 0]]),
np.array([[0, 0], [1, 0]]), # note the duplicate
np.array([[0, 1], [1, 0]]),
np.array([[0, 2], [0, 0]]), # and it continues on in this vein
]
for ex, actual in zip(
expected,
map(as_array, all_double_mods(g)),
):
assert_array_equal(ex, actual)
def test_many_mods(self):
self.assertEqual(40, len(list(all_single_mods(self.g))))
self.assertEqual(1_600, len(list(all_double_mods(self.g))))
self.assertEqual(1_600, len(list(all_mods(self.g, 2))))
self.assertEqual(64_000, len(list(all_mods(self.g, 3))))
self.assertEqual(2_560_000, len(list(all_mods(self.g, 4))))
One could quibble about the fact that
it produces duplicates, since inner and outer loops
know nothing of one another.
It feels like this algorithm wants to use an
itertools.combinations
approach, generating all modifications in lexicographic order.
