Programming in Python (Blender): I want to create a square and print all vertices (A;B;C;D) into my console on top of a given Vector. The square should be orthogonal to this vector, like this: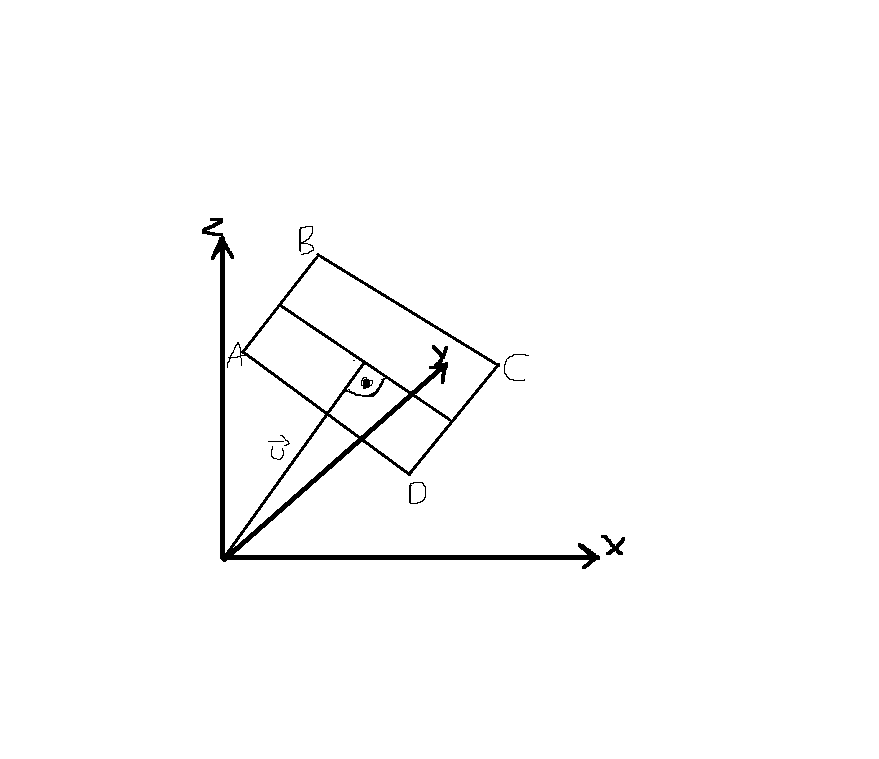

def create_verts_around_point(radius, vert):
    # given Vector
    vec = np.array([vert[0], vert[1], vert[2]])

    # side_length of square
    side_length = radius

    # Vctor x-direction (1,0,0)
    x_vec = np.array([1,0,0])

    # Vekctor  y-direction (0,1,0)
    y_vec = np.array([0,1,0])

    # Vector z-direction (0,0,1)
    z_vec = np.array([0,0,1])

    p1 = vec   (side_length/2) * x_vec   (side_length/2) * y_vec   (side_length/2) * z_vec
    p2 = vec - (side_length/2) * x_vec   (side_length/2) * y_vec   (side_length/2) * z_vec
    p3 = vec - (side_length/2) * x_vec - (side_length/2) * y_vec   (side_length/2) * z_vec
    p4 = vec   (side_length/2) * x_vec - (side_length/2) * y_vec   (side_length/2) * z_vec

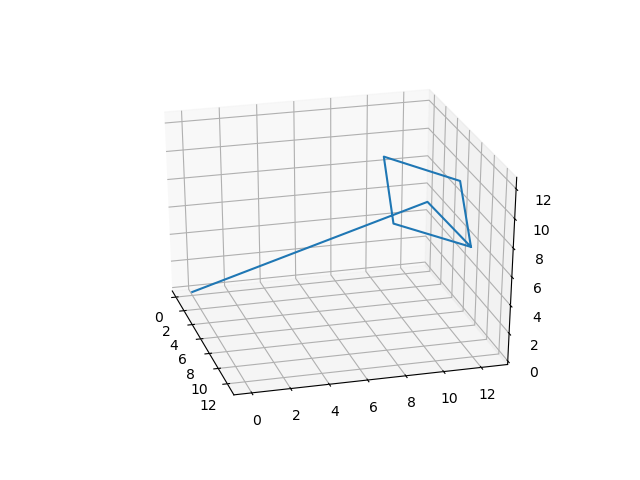
But my output looks like this in the end (Square is always parallel to my x-axis and y-axis):

CodePudding user response：

I don't think you're really thinking about this problem in 3D, but see if this is close.

I create a square, perpendicular to the X axis. I then rotate that square based on the angles in x, y, and z. I then position the square at the end of the vector and plot it. I add plot points for the origin and the end of the vector, and I duplicate the last point in the square do it draws all the lines.

import math
import numpy as np
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt

def create_verts_around_point(sides, vert):

    x0, y0, z0 = vert

    # Here is the unrotated square.

    half = sides/2
    square = [ 
        [0, -half,-half],
        [0, -half, half],
        [0,  half, half],
        [0,  half,-half],
    ]

    # Now find the rotation in each direction.

    thetax = math.atan2( z0, y0 )
    thetay = math.atan2( z0, x0 )
    thetaz = math.atan2( y0, x0 )

    # Now rotate the cube, first in x.

    cubes = []
    txcos = math.cos(thetax)
    txsin = math.sin(thetax)
    tycos = math.cos(thetay)
    tysin = math.sin(thetay)
    tzcos = math.cos(thetaz)
    tzsin = math.sin(thetaz)
    for x,y,z in square:
        x,y,z = (x, y * txcos - z * txsin, y * txsin   z * txcos)
        x,y,z = (x * txcos - z * txsin, y, x * txsin   z * txcos)
        x,y,z = (x * txcos - y * txsin, x * txsin   y * txcos, z)
        cubes.append( (x0 x, y0 y, z0 z) )

    return cubes

point = (10,10,10)
square = create_verts_around_point(5, point)
points = [(0,0,0),point]   square   [square[0]]
x =  [p[0] for p in points]
y =  [p[1] for p in points]
z =  [p[2] for p in points]

ax = plt.figure().add_subplot(111, projection='3d')
ax.plot( x, y, z )
plt.show()

Output: