How to make surrounding average and basic calculations based on numpy neighboring cells-CodePudding

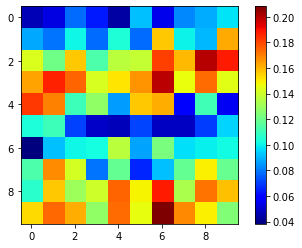
I have a 10 by 10 numpy array. For every cell in the array (as depicted in the snapshot below), I wanted to make calculations based on left, right, top, and bottom neighboring cells, as well as a weighted moving average window based on the surrounding grid cells around each cell in the numpy array (based on its i and j index). I was not sure how to account for grid cells that are located at the edges (boundaries and corners, as they only have a partial of the window kernel around them). Is there any pythonic way to perform these types of tasks? For the weighted_moving_average, the 8 immediate surrounding cells should have a 70% (stronger) whereas the not_immediate sorounding cells (12) should have 30% weights (weaker).

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

noisy_data = [[0.0467251, 0.0529133, 0.0775945, 0.0640082, 0.0439774, 0.0915829,
        0.0547699, 0.0826791, 0.0883616, 0.0977739],
       [0.0875183, 0.0790368, 0.101146 , 0.0777582, 0.104289 , 0.0775479,
        0.156569 , 0.0999909, 0.0905242, 0.161871 ],
       [0.1427   , 0.1211   , 0.15661  , 0.113337 , 0.135986 , 0.1384   ,
        0.181515 , 0.159102 , 0.200004 , 0.187535 ],
       [0.163381 , 0.186425 , 0.174798 , 0.14191  , 0.1514   , 0.166044 ,
        0.199063 , 0.146319 , 0.173303 , 0.144067 ],
       [0.182485 , 0.16901  , 0.11     , 0.127162 , 0.0858656, 0.1564   ,
        0.161187 , 0.0588985, 0.110706 , 0.0560944],
       [0.103804 , 0.109948 , 0.0707144, 0.0493536, 0.0471329, 0.0708205,
        0.048201 , 0.0487304, 0.069967 , 0.0947939],
       [0.0382397, 0.0918   , 0.101197 , 0.102453 , 0.135943 , 0.0867575,
        0.123071 , 0.0970329, 0.099906 , 0.101536 ],
       [0.113361 , 0.167597 , 0.141526 , 0.0792396, 0.118    , 0.065764 ,
        0.0915817, 0.1183   , 0.149376 , 0.118608 ],
       [0.10647  , 0.1566   , 0.1303   , 0.139754 , 0.174465 , 0.148458 ,
        0.187625 , 0.132805 , 0.171687 , 0.158161 ],
       [0.15319  , 0.174204 , 0.161628 , 0.127377 , 0.173368 , 0.145292 ,
        0.208068 , 0.168076 , 0.14961  , 0.124334 ]]

noisy_data = np.array(noisy_data).reshape(10, 10)

plt.imshow(noisy_data, cmap ="jet")
plt.colorbar()


new_df = pd.DataFrame()
new_df['left_neighboring_index') = [(np.abs(noisy_data[i-1] -noisy_data[i]))/(noisy_data[i-1)          noisy_data[i])  for i in noisy_data]

new_df['right_neighboring_index') = [(np.abs(noisy_data[i 1] -noisy_data[i]))/(noisy_data[i 1)    noisy_data[i])  for i in noisy_data]

new_df['bottom_neighboring_index') = [(np.abs(noisy_data[j-1] -noisy_data[j]))/(noisy_data[j-1)   noisy_data[j])  for i in noisy_data]

new_df['top_neighboring_index') = [(np.abs(noisy_data[j 1] -noisy_data[j]))/(noisy_data[j 1)   noisy_data[j])  for i in noisy_data]

new_df['weighted_moving_average_size_20_(8 12)') = ...?

CodePudding user response：

I think what you're looking for is what is known as a convolution. In a convolution on a matrix, a kernel (smaller matrix) is swept across the matrix.

I can try to explain this but I rather suggest you watch this

There are several ways to deal with boundary cells (aslo explained in the video I think). For this you can use the boundary argument in the convolve2D function (see documentation).

CodePudding user response：

You are trying to do operation similar to 2D convolution but not exactly convolution. In convolution, we do multiply with a kernel and then sum the resulting value and place it in each cell. You want the average of the product to be placed in the cell instead.

def surr_avg(img, kernel):
    kernel_shape = kernel.shape
    # get the sliding window view of the image.
    sub_matrices = np.lib.stride_tricks.sliding_window_view(img, kernel_shape)
    # Multiply kernel with each window of img using einsum.
    conv = np.einsum('kl,ijkl->ijkl',kernel,sub_matrices)
    # find the reduced mean along the last two axis.
    return conv.mean(axis=(-1,-2))

For simple average:

k = np.array([[1,1,1],
              [1,0,1], 
              [1,1,1]])
avg = surr_avg(a, k)

For weighted average:

wk = np.array([
    [.3, .3, .3, .3, .3],
    [.3, .7, .7, .7, .3],
    [.3, .7, .0, .7, .3],
    [.3, .7, .7, .7, .3],
    [.3, .3, .3, .3, .3]
])
wk /= wk.sum()
wght_avg = surr_avg(a, wk)