The 
How I tried and failed to solve this problem.
Approach I.
Iterate over every point and find the min and max of x and y.
Then crop to a polygon using these coordinates.
The problem is that algorithm on an example image would remove the top part of the image but there is no need to because we 'missed' top left and right boxes.
Approach II.
Try to choose to crop only one side at a time, because usually in my dataset things to exclude are on one side. e.g. remove top 100px
So I calculated the min and max of x and y like before.
Then the calculated area of every possible cut - left, right, top, bottom and choose one with the smallest area.
This approach failed pretty quickly when there are boxes on two sides of picture like left and right
CodePudding user response:
Here's a potential solution to find the bounding box contour with the largest surface area. We have two requirements:
- Largest bounding box is not intersecting with any other box
- Largest bounding box is not inside another box
Essentially we can reword the two requirements to this:
- Given C1 and C2, determine if C1 and C2 intersect
- Given C1 and C2, check if there is a point from C1 in C2
To solve #1, we can create a contour_intersect function that uses a bitwise AND operation with 
Answer:
Contour
Next we add two additional contours. Contour #3 will represent the intersection scenario and contour #4 will represent the inside contour scenario.
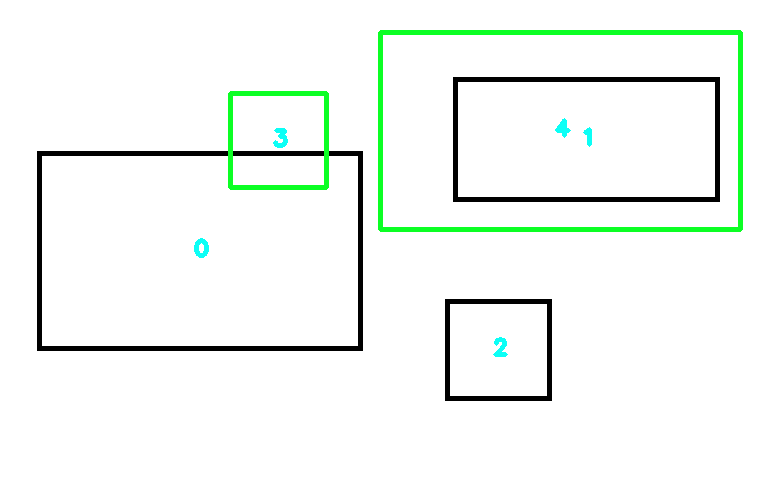
Answer:
Contour
Contour
Contour
To solve this problem, we find contours then sort using contour area from largest to smallest. Next, we compare this contour with all other contours and check the two cases. If either case fails, we dump the current contour and move onto the next largest contour. The first contour that passes both tests for all other contours is our largest bounding box contour. Normally, contour #0 would be our largest but it fails the intersection test. We then move onto contour #1 but this fails the inside test. Thus the last remaining contour that passes both tests is contour #2.
import cv2
import numpy as np
def contour_intersect(original_image, contour1, contour2):
contours = [contour1, contour2]
blank = np.zeros(original_image.shape[0:2])
image1 = cv2.drawContours(blank.copy(), contours, 0, 1)
image2 = cv2.drawContours(blank.copy(), contours, 1, 1)
intersection = np.logical_and(image1, image2)
return intersection.any()
def contour_inside(contour1, contour2):
M = cv2.moments(contour1)
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
inside = cv2.pointPolygonTest(contour2, (cx, cy), False)
if inside == 0 or inside == -1:
return False
elif inside == 1:
return True
image = cv2.imread('1.png')
original = image.copy()
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
thresh = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV cv2.THRESH_OTSU)[1]
cnts = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts[0] if len(cnts) == 2 else cnts[1]
sorted_cnts = sorted(cnts, key=lambda x: cv2.contourArea(x), reverse=True)
intersect_contour = np.array([[[230, 93]], [[230, 187]], [[326, 187]], [[326, 93]]])
sorted_cnts.append(intersect_contour)
cv2.drawContours(original, [intersect_contour], -1, (36,255,12), 3)
inside_contour = np.array([[[380, 32]], [[380, 229]], [[740, 229]], [[740, 32]]])
sorted_cnts.append(inside_contour)
cv2.drawContours(original, [inside_contour], -1, (36,255,12), 3)
for count, c in enumerate(sorted_cnts):
M = cv2.moments(c)
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
cv2.putText(original, str(count), (cx-5, cy 5), cv2.FONT_HERSHEY_SIMPLEX, 0.7, (246,255,12), 3)
largest_contour_name = ""
largest_contour = ""
contours_length = len(sorted_cnts)
for i1 in range(contours_length):
found = True
for i2 in range(i1 1, contours_length):
c1 = sorted_cnts[i1]
c2 = sorted_cnts[i2]
if contour_intersect(original, c1, c2) or contour_inside(c1, c2):
print('Contour #{} has failed test'.format(i1))
found = False
continue
if found:
largest_contour_name = i1
largest_contour = sorted_cnts[i1]
break
print('Contour #{} is the largest'.format(largest_contour_name))
print(largest_contour)
cv2.imshow('thresh', thresh)
cv2.imshow('image', image)
cv2.imshow('original', original)
cv2.waitKey()
Note: The assumption is that you have an array of contours from cv2.findContours() with the format like this example:
cnts = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts[0] if len(cnts) == 2 else cnts[1]
sorted_cnts = sorted(cnts, key=lambda x: cv2.contourArea(x), reverse=True)
for c in sorted_cnts:
print(c)
print(type(c))
x,y,w,h = cv2.boundingRect(c)
print((x,y,w,h))
Output
[[[230 93]]
[[230 187]]
[[326 187]]
[[326 93]]]
<class 'numpy.ndarray'>
(230, 93, 97, 95)
Performance note: The intersection check function suffers on the performance side since it creates three copies of the input image to draw the contours and may be slower when it comes to execution time with a greater number of contours or a larger input image size. I'll leave this optimization step to you!
CodePudding user response:
Consider a full recangle (initially the whole picture) and take away one excluded box. You will get 2x2x2x2=16 possible rectangular subdivisions, for example this one.
┌────────────────────────┐
│ │
│ │
├───────┬───────┬────────┤
│ │ exc │ │
│ │ lude │ │
│ ├───────┴────────┤
│ │ │
│ │ │
└───────┴────────────────┘
For each box in the subdivision, take away the next excluded box.
Do this N times, and take the biggest box of the final step.
CodePudding user response:
You can use the 
CodePudding user response:
Assumption: you want the largest box from your array that complies with your rules, and it is not the largest NEW bounding box that complies.
This is pseudo code, you still have to fill in blanks
int largestBoxIndex = -1;
int largestBoxArea = -1;
for (i=0; i<allBoxes[].length; i )
{
box CurrentBox = allBoxes[i];
bool isComply = false;
for (j=0; j<allBoxes[].length; j )
{
isComply = false;
if(i==j) break;
ComparedBox = allBoxes[j]
if (isIntersected(CurrentBox, ComparedBox)) break;
if (isInside(CurrentBox, ComparedBox)) break;
isComply = true;
}
if(isComply)
if(Area(allBoxes[i]) > largestBoxArea)
{
largestBoxArea = Area(allBoxes[i]):
largestBoxIndex =i;
}
}
if(largestBoxIndex != -1)
largestBoxIndex;//this is the largest box
CodePudding user response:
A simple mathematical solution to the problem
Suppose you are given 5 rectangles as shown below:
rects = [[100, 100, 200, 200],
[200, 200, 200, 200],
[200, 500, 200, 200],
[350, 50, 150, 200],
[500, 400, 200, 300]]
Note that the format of these rectangles is: [x, y, width, height]
Where, (x, y) is the coordinate of the top left corner of the rectangle, and width & height are the width and height of the rectangle respectively. You will have to covert your coordinates in this format first.
3 out of these 5 are intersecting.
Now what we will do is iterate over these rectangles one by one, and for each rectangle, find the intersection of this rectangle with the other rectangles one by one. If any rectangle is found to be intersecting with any of the other rectangles, then we'll set the flag value for the two rectangles as 0. If a rectangle is found not to be intersecting with any other rectangle, then its flag value will be set to 1. (Default flag value is -1). Finally, we'll find the rectangle of the greatest area among the rectangles with flag value 1.
Let's see the code for finding the intersection area of the two rectangles:
def Intersection(Rect1, Rect2):
x = max(Rect1[0], Rect2[0])
y = max(Rect1[1], Rect2[1])
w = min(Rect1[0] Rect1[2], Rect2[0] Rect2[2]) - x
h = min(Rect1[1] Rect1[3], Rect2[1] Rect2[3]) - y
if w < 0 or h < 0:
return None
return [x, y, w, h]
This function will return None if there is no intersecting area between these rectangles or it will return the coordinates of the intersection rectangle(Ignore this value for the current problem. This might be helpful in other problems).
Now, let's have a look at the algorithm.
n = len(rects)
flag = [-1]*n
for i in range(n):
if flag[i] == 0:
continue
isIntersecting = False
for j in range(n):
if i == j or flag[j] == 1:
continue
Int_Rect = Intersection(rects[i], rects[j])
if Int_Rect is not None:
isIntersecting = True
flag[j] = 0
flag[i] = 0
break
if isIntersecting == False:
flag[i] = 1
maxRect = None
maxArea = -1
for i in range(n):
if flag[i] == 1:
if rects[i][2] * rects[i][3] > maxArea:
maxRect = rects[i]
maxArea = rects[i][2] * rects[i][3]
print(maxRect)
Note: Add the "excluded areas" rectangle coordinates to the rects list and assign their flag value as 0 to avoid them from getting selected as the maximum area rectangle.
This solution does not involve any images so it will be the fastest algorithm unless it is optimized.
CodePudding user response:
Find the biggest square in numpy array
Maybe this would help? If you know the size of the whole area you can calculate the biggest box within numpy array. If you set all your given boxes to 1 and your whole area to 0 you need to find the largest area that is unique and not 1.
