Given n samples from a uniform distribution [0,d], how would you estimate d?-CodePudding

I believe there are two approaches to solving this problem.

One would be to take the MAX from the sample set and the other would be to take 2 x the sample mean.

I found a solution online that attempted to create these distribution to compare the two however, it was written unusually (for statements followed the actual statement). I attempted to rewrite it but something about my code is off. It doesn't seem like it is running the function multiple times and comparing the result as the sample size increases. Any help is appreciated.

My code


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def sample_random_normal(n = 100):
    for i in range(1,100):
        for j in [np.random.uniform(0, n, size = i).astype(int)]:
            return np.array([np.array([max(j), 2*np.mean(j)])])

def repeat_experiment():
    for _ in range(1,100):
        experiments = np.array([sample_random_normal()])
        return experiments.mean(axis = 0)

result = repeat_experiment()
df = pd.DataFrame(result)
df.columns = ['max_value', '2*mean']
df['k'] = pd.Series(range(1,100))
df['actual_value'] = 100
df['max_value-actual-value'] = df['max_value'] - df['actual_value']
df['2*mean-actual_value'] = df['2*mean'] - df['actual_value']
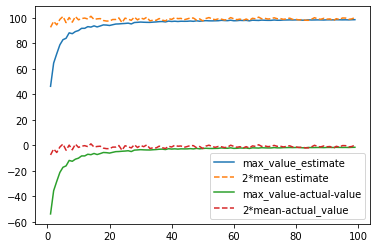
plt.plot(df['k'], df['max_value'], linestyle = 'solid', label = 'max_value_estimate')
plt.plot(df['k'], df['2*mean'], linestyle = 'dashed', label = '2*mean estimate')
plt.plot(df['k'], df['max_value-actual-value'], linestyle = 'solid', label = 'max_value_estimate')
plt.plot(df['k'], df['2*mean-actual_value'], linestyle = 'dashed', label = '2*mean estimate')
plt.legend()
plt.show()

Original Code

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def sample_random_normal(n = 100):
    return np.array([np.array([max(j), 2*np.mean(j)]) for j in [np.random.uniform(0, n, size=i).astype(int) for i in range(1, 100)]])

def repeat_experiment():
    experiments = np.array([sample_random_normal() for _ in range(100)])
    return experiments.mean(axis = 0)

result = repeat_experiment()
df = pd.DataFrame(result)
df.columns = ['max_value', '2*mean']
df['k'] = range(1, 100)
df['actual_value'] = 100
df['max_value-actual-value'] = df['max_value'] - df['actual_value']
df['2*mean-actual-value'] = df['2*mean'] - df['actual_value']
plt.plot(df['k'], df['max_value'], linestyle='solid', label='max_value_estimate')
plt.plot(df['k'], df['2*mean'], linestyle='dashed', label ='2*mean estimate')
plt.legend()
plt.show()

CodePudding user response：

Look at here:

def sample_random_normal(n = 100):
    for i in range(1,100):
        for j in [np.random.uniform(0, n, size = i).astype(int)]:
            return np.array([np.array([max(j), 2*np.mean(j)])])

For the first iand j in your range, your function finds a return statement and stops. A correction would be:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def sample_random_normal(n = 100):
        samples = [np.random.uniform(0, n, size = i).astype(int) for i in range(1,100)]
        return np.array([np.array([max(j), 2*np.mean(j)]) for j in samples])

def repeat_experiment():
        experiments = np.array([sample_random_normal() for _ in range(100)])
        return experiments.mean(axis = 0)

result = repeat_experiment()
df = pd.DataFrame(result)
df.columns = ['max_value', '2*mean']
df['k'] = pd.Series(range(1,100))
df['actual_value'] = 100
df['max_value-actual-value'] = df['max_value'] - df['actual_value']
df['2*mean-actual_value'] = df['2*mean'] - df['actual_value']
plt.plot(df['k'], df['max_value'], linestyle = 'solid', label = 'max_value_estimate')
plt.plot(df['k'], df['2*mean'], linestyle = 'dashed', label = '2*mean estimate')
plt.plot(df['k'], df['max_value-actual-value'], linestyle = 'solid', label = 'max_value-actual-value')
plt.plot(df['k'], df['2*mean-actual_value'], linestyle = 'dashed', label = '2*mean-actual_value')
plt.legend()
plt.show()

And the results are:

And you just showed these two estimators are consistent. Notice, however, that the maximum estimator is not unbiased, where 2 times the mean is. This is more of a math/statistic question, however; if interested, see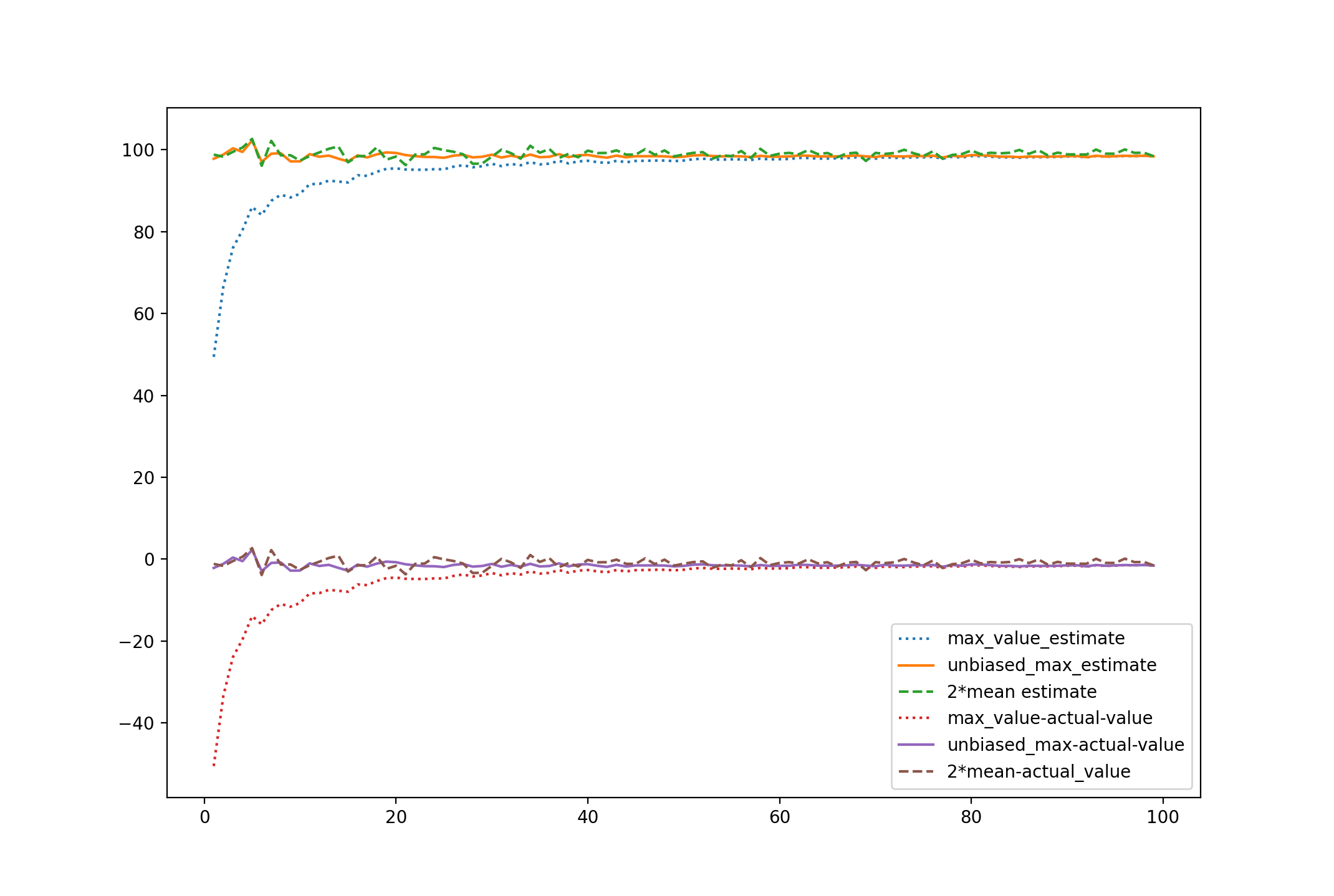

As you can see, the scaled max estimator dominates the performance of the other two, lacking the bias of the vanilla max and having less variability than doubling the sample mean.