How to count contour (inside value, outside 0) pixels on a given 2d array?-CodePudding

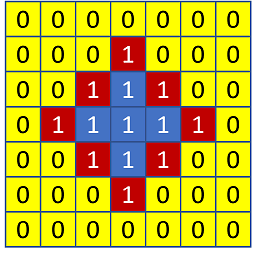
I have the following task to solve. I have an image (numpy array) where everything that is not the main object is 0 and the main object has some pixel counts all around (let's set all of them to 1).

What I need is to get the number of all the pixels on the contour (red squares with 1 as the value) of this object. The objects can have different forms. Is there any way to achieve it?

OBS: The goal is to have a method that would be able to adapt to the shape of the figure, because it would be run on multiple images simultaneously.

CodePudding user response：

This is interesting and I got an elegant solution for you.

Since we can agree that contour is defined as np.array value that is greater than 0 and have at least 1 neighbor with a value of 0 we can solve it pretty stright forward and make sure it is ready for every single image you will get for life (in an Numpy array, of course...)

import numpy as np 

image_pxs = np.array([[0, 0, 0, 0, 0, 0, 0],
                     [0, 0, 0, 1, 0, 0, 0],
                     [0, 0, 1, 1, 1, 0, 0],
                     [0, 1, 1, 1, 1, 1, 0],
                     [0, 0, 1, 1, 1, 0, 0],
                     [0, 0, 0, 1, 0, 0, 0],
                     [0, 0, 0, 0, 0, 0, 0]])


def get_contour(two_d_arr):
    contour_pxs = 0
    # Iterate of np:
    for i, row in enumerate(two_d_arr):
        for j, pixel in enumerate(row):
            # Check neighbors
            up = two_d_arr[i-1][j] == 0 if i > 0 else False
            down = two_d_arr[i 1][j] == 0 if i < len(image_pxs)-1 else False
            left = two_d_arr[i][j-1] == 0 if j > 0 else False
            right = two_d_arr[i][j 1] == 0 if j < len(row)-1 else False
            # Count distinct neighbors (empty / not empty)
            sub_contour = len(list(set([up, down, left, right])))
            # If at least 1 neighbor is empty and current value > 0 it is the contour
            if sub_contour > 1 and pixel > 0:
                # Add the number of pixels in i, j
                contour_pxs  = pixel
    return contour_pxs
            
print(get_contour(image_pxs))

The output is of course 8:

8
[Finished in 97ms]

CodePudding user response：

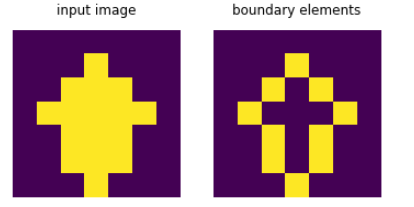
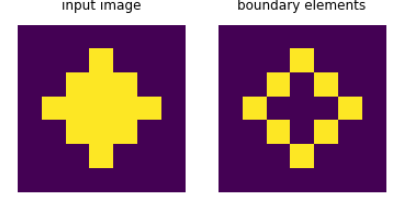
I propose a similar solution to @user2640045 using convolution. We can slide a filter over the array that counts the number of neighbours (left, right, top, bottom):

import numpy as np
from scipy import signal
a = np.array(
    [
     [0, 0, 0, 0, 0, 0, 0], 
     [0, 0, 0, 1, 0, 0, 0], 
     [0, 0, 1, 1, 1, 0, 0], 
     [0, 1, 1, 1, 1, 1, 0], 
     [0, 0, 1, 1, 1, 0, 0], 
     [0, 0, 0, 1, 0, 0, 0], 
     [0, 0, 0, 0, 0, 0, 0], 
    ]
)

filter = np.array([[0, 1, 0],
                   [1, 0, 1],
                   [0, 1, 0]])

Now we convolve the image array with the filter and :

conv = signal.convolve2d(a, filter, mode='same')

Every element that has more than zero and less than four neighbors while being active itself is a boundary element:

bounds = a * np.logical_and(conv > 0, conv < 4)

We can sum this up to get the number of boundary elements:

>>> bounds.sum()
8

Here are 2 example inputs:

CodePudding user response：

Yes. What you're looking for is called convolution. It slights around a small array of weights multiplies the values under the weights with the weights and sums up. If in your case you pick weights of shape 3 by 3 of ones you get the sums of neighbors.

from scipy import signal
import numpy as np

arr = np.fromfunction(lambda i,j: (i-3)**2 (j-3)**2 < 5,(7,7)).astype('float')
conv = signal.convolve2d(arr,np.ones((3,3), dtype='float'),mode='same')
conv

gives

array([[0., 0., 1., 1., 1., 0., 0.],
       [0., 1., 3., 4., 3., 1., 0.],
       [1., 3., 6., 7., 6., 3., 1.],
       [1., 4., 7., 9., 7., 4., 1.],
       [1., 3., 6., 7., 6., 3., 1.],
       [0., 1., 3., 4., 3., 1., 0.],
       [0., 0., 1., 1., 1., 0., 0.]])

Since boundary points have between 4 and 6 neighbors you get your desired result by

((3 < conv) & (conv < 7)).sum()

As expected it is 8. Disclaimer: This works for convex shapes if you're interested in concave ones we'll have to come up with a smarter convolution but it should still work.