Solve ODEs with Numba-CodePudding

I'm trying to make my ODEs solver faster with Numba, but the following code throws a Typing Error:

    import numpy as np
    import matplotlib.pyplot as plt
    from numba import njit

    @njit
    def pend(t, y, b, c):
        theta, omega = y
        dydt = np.array([omega, -b*omega - c*np.sin(theta)])
        return dydt

    @njit
    def rungeStep(f, t, y0, tau, params):
        k1 = tau * f(t, y0, *params)
        k2 = tau * f(t, y0   k1 / 2, *params)
        k3 = tau * f(t, y0   k2 / 2, *params)
        k4 = tau * f(t, y0   k3, *params)
        return (k1   2 * k2   2 * k3   k4) / 6
    @njit
    def integrate(f, t0, y0, tEnd, h, params):
        ys = y0.copy()
        t = np.array(t0)
        while t0 <= tEnd:
            y0  = rungeStep(f, t0, y0[0], h, params)
            t0  = h
            ys = np.concatenate((ys, y0), axis=0)
            t = np.append(t, t0)
        return t, ys.T

    args = (0.25, 5)
    y0 = np.array([[np.pi - 0.1, 0.0]])
    t, y = integrate(pend, 0, y0, 10, 1, args)

This results in:

    TypingError: Failed in nopython mode pipeline (step: nopython frontend)
    Cannot unify array(int64, 0d, C) and array(int64, 1d, C) for 't.2', defined at <ipython-input-56-38d2ea70b889> (6)
    
    File "<ipython-input-56-38d2ea70b889>", line 6:
    def inagrate(f, t0, y0, tEnd, h, params):
        <source elided>
        while t0 <= tEnd:
            y0  = rungeStep(f, t0, y0[0], h, params)
            ^
    
    During: typing of assignment at <ipython-input-56-38d2ea70b889> (6)
    
    File "<ipython-input-56-38d2ea70b889>", line 6:
    def inagrate(f, t0, y0, tEnd, h, params):
        <source elided>
        while t0 <= tEnd:
            y0  = rungeStep(f, t0, y0[0], h, params)
            ^

Without the njit-decorator it works fine. Can anybody help me please?

CodePudding user response：

One should get the same error without JIT, but perhaps the broadcasting rules are flexible enough. Your y0 is a 2d array, what you pass to rungeStep (of the Heun-Kutta method) is a 1d array, as is its return value. So you can not use that result immediately to update y0, you would have to update y0[0]. But then the question is why introduce this complexity in the first place.

Numpy arrays are optimized as fixed-size objects, appending to them requires memory allocation and copying in every instance, which is slower than appending to lists, where re-allocation is done with a (growing) reserve. Numba-JIT appears to have a problem with transforming lists of numpy arrays to 2d numpy arrays. What works is to manually downgrade the arrays to simple lists. With some trial-and-error I got the following code running (only repeating pieces with changes):

@njit
def rungeStep(f, t, y0, tau, params):
    k1 = tau * f(t, y0, *params)
    k2 = tau * f(t   tau/2, y0   k1 / 2, *params)
    k3 = tau * f(t   tau/2, y0   k2 / 2, *params)
    k4 = tau * f(t   tau, y0   k3, *params)
    return (k1   2 * k2   2 * k3   k4) / 6
@njit
def integrate(f, t0, y0, tEnd, h, params):
    ys = [list(y0)]
    t = [t0]
    while t0 <= tEnd:
        y0  = rungeStep(f, t0, y0, h, params)
        t0  = h
        ys.append(list(y0))
        t.append(t0)
    return np.array(t), np.array(ys).T

args = (0.25, 5.0)
y0 = np.array([np.pi - 0.1, 0.0])
t, y = integrate(pend, 0, y0, 10, 1e-1, args)

Note that your RK4 implementation had some omissions, not critical here but an error source for time-depending ODE examples.

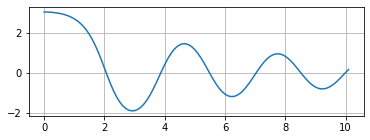
Plotting the result gives the reasonable graph