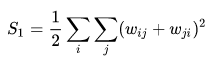Calculate the S1 sum for variance of Moran's I-CodePudding

I would like to calculate the S1 term for the variance of Moran's I. The following is the formula to calculate the S1

where w_{ij} is an element in the spatial weights matrix.

My spatial weights matrix is as following:-

structure(c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0.111111111111111, 0.1, 0.1, 0.166666666666667,
0, 0.1, 0.111111111111111, 0.125, 0.166666666666667, 0, 0, 0.1,
0.111111111111111, 0, 0, 0.166666666666667, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0.0909090909090909,
0, 0, 0.1, 0.1, 0.166666666666667, 0, 0.1, 0.111111111111111,
0.125, 0.166666666666667, 0, 0, 0.1, 0, 0, 0, 0, 0, 0, 0.0909090909090909,
0, 0.111111111111111, 0, 0.1, 0, 0, 0.1, 0.111111111111111, 0.125,
0.166666666666667, 0, 0, 0.1, 0.111111111111111, 0, 0, 0.166666666666667,
0, 0, 0.0909090909090909, 0, 0.111111111111111, 0.1, 0, 0, 0.333333333333333,
0.1, 0.111111111111111, 0.125, 0, 0, 0, 0.1, 0.111111111111111,
0, 0, 0.166666666666667, 0, 0, 0.0909090909090909, 0, 0.111111111111111,
0, 0, 0, 0, 0.1, 0.111111111111111, 0, 0.166666666666667, 0,
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0.1, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0.111111111111111, 0, 0, 0.166666666666667, 0, 0, 0.0909090909090909,
0, 0.111111111111111, 0.1, 0.1, 0.166666666666667, 0, 0, 0.111111111111111,
0.125, 0.166666666666667, 0, 0, 0.1, 0.111111111111111, 0, 0,
0, 0, 0, 0.0909090909090909, 0, 0.111111111111111, 0.1, 0.1,
0.166666666666667, 0, 0.1, 0, 0.125, 0, 0, 0, 0.1, 0.111111111111111,
0, 0, 0, 0, 0, 0.0909090909090909, 0, 0.111111111111111, 0.1,
0.1, 0, 0, 0.1, 0.111111111111111, 0, 0, 0, 0, 0.1, 0.111111111111111,
0, 0, 0, 0, 0, 0.0909090909090909, 0, 0.111111111111111, 0.1,
0, 0.166666666666667, 0, 0.1, 0, 0, 0, 0, 0, 0.1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0.0909090909090909, 0, 0.111111111111111, 0.1, 0.1, 0, 0, 0.1,
0.111111111111111, 0.125, 0.166666666666667, 0, 0, 0, 0.111111111111111,
0, 0, 0.166666666666667, 0, 0, 0.0909090909090909, 0, 0, 0.1,
0.1, 0, 0.333333333333333, 0.1, 0.111111111111111, 0.125, 0,
0, 0, 0.1, 0, 0, 0, 0.166666666666667, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.166666666666667,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.0909090909090909,
0, 0, 0.1, 0.1, 0, 0.333333333333333, 0, 0, 0, 0, 0, 0, 0.1,
0.111111111111111, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0), .Dim = c(20L, 20L), .Dimnames = list(
    c("AUS", "BEL", "CAN", "CHE", "DEU", "DNK", "ESP", "FIN",
    "FRA", "GBR", "IRL", "ITA", "JPN", "KOR", "NLD", "NOR", "NZL",
    "PRT", "SWE", "USA"), c("AUS", "BEL", "CAN", "CHE", "DEU",
    "DNK", "ESP", "FIN", "FRA", "GBR", "IRL", "ITA", "JPN", "KOR",
    "NLD", "NOR", "NZL", "PRT", "SWE", "USA")))

I can do this by using a for loop within a for loop, but I am thinking that there might be a more efficient way to do this. Maybe using lapply or something else.

Thanks in advance.

CodePudding user response：

Define a squared sum function and use outer.

squared_sum <- function(x, y) (x   y)^2
sum(outer(W, W, squared_sum))/2
#[1] 3037.03

CodePudding user response：

Using expand.grid

squared_sum <- function(x, y) (x   y)^2
with(expand.grid(W, W) , sum(squared_sum(Var1, Var2)))/2
[1] 3037.03

CodePudding user response：

for me, the solution looks like this

set.seed(1)
m <- matrix(sample(c(0, 1), size = 16, replace = TRUE), nrow = 4) 
diag(m) <- 0
m
#>      [,1] [,2] [,3] [,4]
#> [1,]    0    1    1    0
#> [2,]    1    0    1    0
#> [3,]    0    0    0    0
#> [4,]    0    0    0    0
S1 <- 0.5 * sum((m   t(m))^2)
S1
#> [1] 6

^{Created on 2021-10-07 by the reprex package (v2.0.1)}