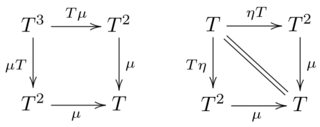
The laws for monoids in the category of endofunctors are:
And the Haskell monad laws are:
Left identity: return a >>= k = k a
Right identity: m >>= return = m
Associativity: m >>= (\x -> k x >>= h) = (m >>= k) >>= h
I'm assuming the latter is derived from the former, but how so? The diagrams basically say
join (join x) = join (fmap join x)
join (return x) = x
join (fmap return x) = x
How are these equivalent to the Haskell monad laws?
CodePudding user response:
To show the >>=-monad laws from the join-monad laws, one needs to define x >>= y in terms of multiplication (join), unity (return), and functoriality (fmap), so we need to let, by definition,
(x >>= y) = join (fmap y x)
Left identity law
The left identity law then becomes
return a >>= k = k a
By definition of >>=, it is equivalent to
join (fmap k (return a)) = k a
Now, return is a natural transformation I -> T (where I is the identity functor), so fmap_T k . return = return . fmap_I k = return . k. We reduce the law to:
join (return (k a)) = k a
And this follows by the join laws.
Right identity law
The right identity law
m >>= return = m
reduces to, by definition of >>=:
join (fmap return m) = m
which is exactly one of the join laws.
I'll leave the associativity law for you to prove. It should follow using the same tools (join laws, naturality, functoriality).
CodePudding user response:
Phrase the monad laws in terms of the Kleisli composition operator (>=>).
Assuming k :: a -> m b, k' :: b -> m c, k'' :: c -> m d (i.e. k, k', k'' are Kleisli arrows)
- Left identity:
return >=> k = k - Right identity:
k >=> return = k - Associativity:
(k >=> k') >=> k'' = k >=> (k' >=> k'')
It's relatively straightforward from the definition of (>=>) to show that these are equivalent to what you wrote. And you don't need any fancy diagrams or anything: these are literally the monoid laws, with return as the identity and (>=>) as your monoid operation.
The diagram you show in your picture is a different way of thinking about monads. You can equivalently define monads in terms of natural transformations (i.e. join and return) or in terms of composition (i.e. return and (>>=) / (>=>)). The latter approach lends itself to the monoid way of thinking that you're looking for.