Plotting the mean of multiple columns including standard deviation-CodePudding

I have a data set with 8 columns and several rows. The columns contain measurements for different variable (6 in total) under 2 different conditions, each consisting of 4 columns that contain repeated measurements for a particular condition.

Using Searborn, I would like to generate a bar chart displaying the mean and standard deviation of every 4 columns, grouped by index key (i.e. measured variable). The dataframe structure is as follows:

np.random.seed(10)
df = pd.DataFrame({
    'S1_1':np.random.randn(6),
    'S1_2':np.random.randn(6),
    'S1_3':np.random.randn(6),
    'S1_4':np.random.randn(6),
    'S2_1':np.random.randn(6),
    'S2_2':np.random.randn(6),
    'S2_3':np.random.randn(6),
    'S2_4':np.random.randn(6),
    },index= ['var1','var2','var3','var4','var5','var6'])

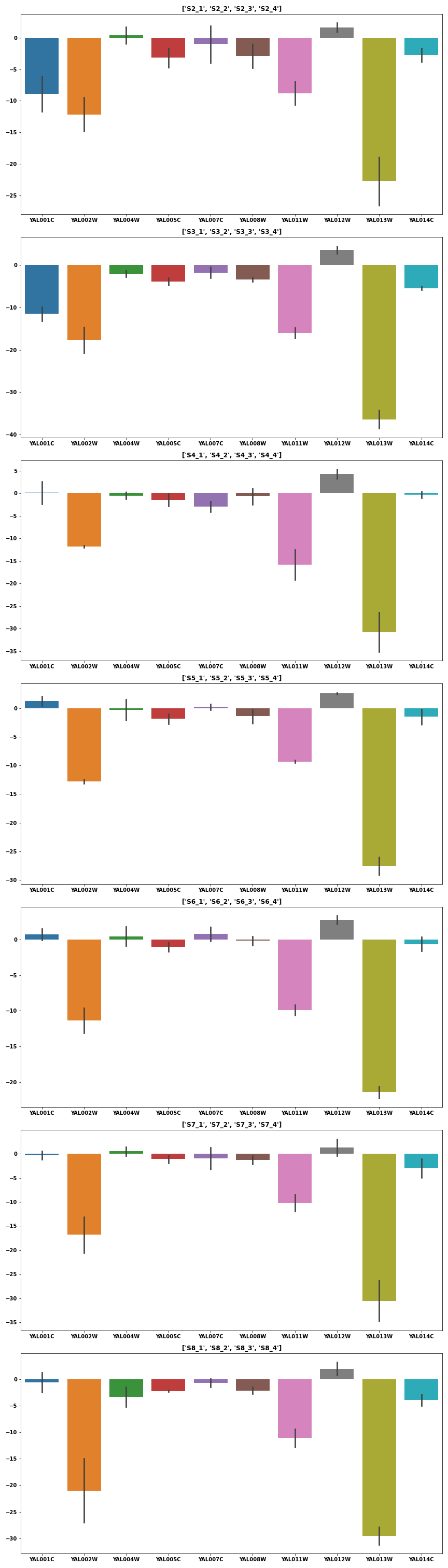
How do I pass to seaborn that I would like only 2 bars, 1 for the first 4 columns and 1 for the second. With each bar displaying the mean (and standard deviation or some other measure of dispersion) across 4 columns.

I was thinking of using multi-indexing, adding a second column level to group the columns into 2 condition,

df.columns = pd.MultiIndex.from_arrays([['Condition 1'] * 4   ['Condition 2'] * 4,df.columns])

but I can't figure out what I should pass to Seaborn to generate the plot I want.

If anyone could point me in the right direction, that would be a great help!

CodePudding user response：

Update Based on Comment

Plotting is all about reshaping the dataframe for the plot API

# still create the groups
l = df.columns
n = 4
groups = [l[i:i n] for i in range(0, len(l), n)]
num_gps = len(groups)

# stack each group and add an id column
data_list = list()
for group in groups:
    id_ = group[0][1]
    data = df[group].copy().T
    data['id_'] = id_
    data_list.append(data)
    
df2 = pd.concat(data_list, axis=0).reset_index()
df2.rename({'index': 'sample'}, axis=1, inplace=True)

# melt df2 into a long form
dfm = df2.melt(id_vars=['sample', 'id_'])

# plot
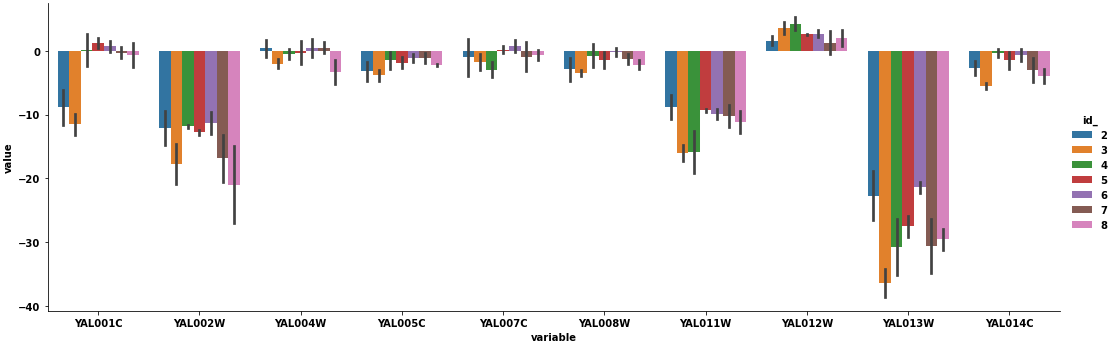
p = sns.catplot(kind='bar', data=dfm, x='variable', y='value', hue='id_', ci='sd', aspect=3)

`df2.head()`

  sample    YAL001C    YAL002W   YAL004W   YAL005C   YAL007C   YAL008W    YAL011W   YAL012W    YAL013W   YAL014C id_
0   S2_1 -13.062716  -8.084685  2.360795 -0.740357  3.086768 -0.117259  -5.678183  2.527573 -17.326287 -1.319402   2
1   S2_2  -5.431474 -12.676807  0.070569 -4.214761 -4.318011 -4.489010 -10.268632  0.691448 -24.189106 -2.343884   2
2   S2_3  -9.365509 -12.281169  0.497772 -3.228236  0.212941 -2.287206 -10.250004  1.111842 -27.811564 -4.329987   2
3   S2_4  -7.582111 -15.587219 -1.286167 -4.531494 -3.090265 -4.718281  -8.933496  2.079757 -21.580854 -2.834441   2
4   S3_1 -12.618254 -20.010779 -2.530541 -3.203072 -2.436503 -2.922565 -15.972632  3.551605 -35.618485 -4.925495   3

`dfm.head()`

  sample id_ variable      value
0   S2_1   2  YAL001C -13.062716
1   S2_2   2  YAL001C  -5.431474
2   S2_3   2  YAL001C  -9.365509
3   S2_4   2  YAL001C  -7.582111
4   S3_1   3  YAL001C -12.618254

Plot Result

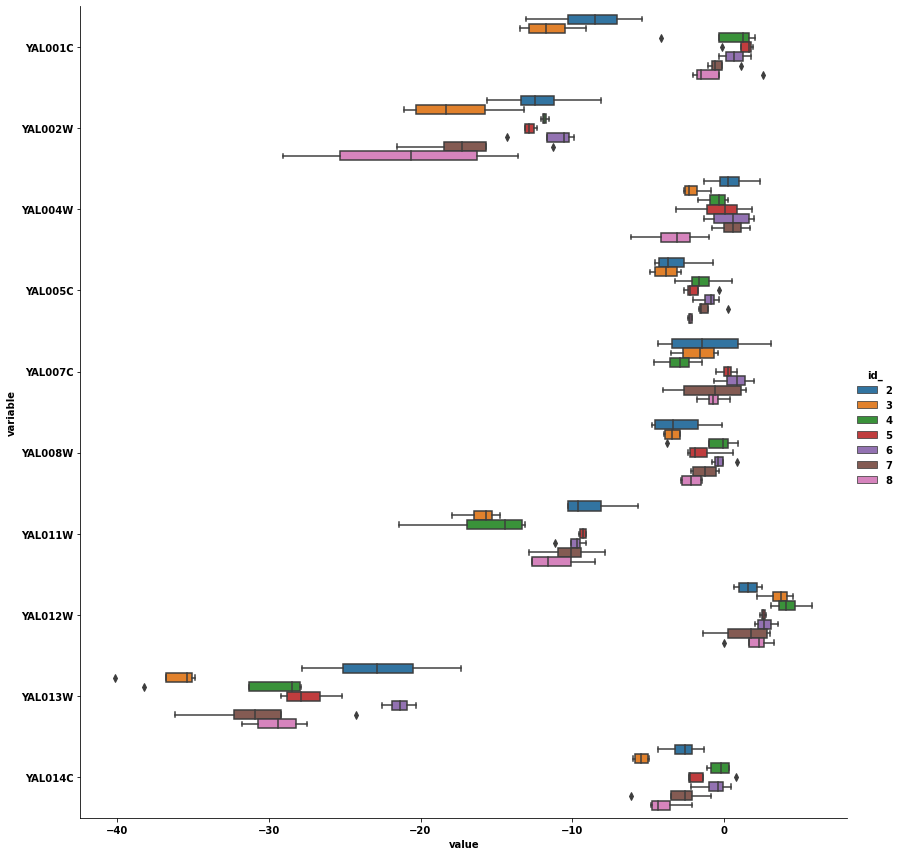
`kind='box'`

A box plot might be a better to convey the distribution

p = sns.catplot(kind='box', data=dfm, y='variable', x='value', hue='id_', height=12)

Original Answer

Use a list comprehension to chunk the columns into groups of 4
- This uses the original, more comprehensive data that was posted. It can be found in