How to determine the points belonging to the distance between two not intersecting lines in space-CodePudding

I have a question that I would like to share with you in case you could help me. I am working on 3D lines and I need to obtain the exact points at which the minimum distance of two intersecting lines is located. Why do I need these points?

Of each one of the infinite lines, I would only be interested in knowing if this minimum distance is in a certain range from that of points on the same line. For example, I have the points P (0,0,0) and Q (10,10,10) of a line r and I would only be interested to know if said minimum distance is in that coordinate interval or not.

To obtain the distance, I use the formula:

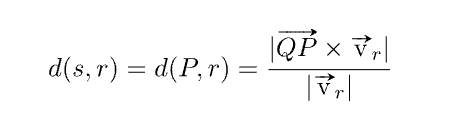
But once said I do not know how to ensure if such a minimum distance is reached within the range of values of P and Q that I comment above.

If anyone has any better ideas on how to check this or knows how to get such points, I would really appreciate it.

CodePudding user response：

If I understand your question right:

for point P get orthogonal projections onto both lines (denominator is not needed if v and w are normalized)

PAproj = A - P   dot(AP, v) / dot(v,v) * v
PBproj = B - P   dot(BP, w) / dot(w,w) * w

Then check that these vectors are anticollinear

 cross(PAproj, PBproj) == 0   
   and 
 dot(PAproj, PBproj) has negative sign

CodePudding user response：

Usually, lines in 3D are specified by the coordinates of one point on the line and the coordinates of one vector aligned (or parallel) to the line. So I am going to assume that what you have as input data is:

1) line s with point S = [xS, yS, zS] on l and a vector u = [u1, u2, u3] aligned with s

2) line r defined by the pair of points P = [xP, yP, zP] and Q = [xQ, yQ, zQ] 

Your goal is to check whether the point on r that is closest to line s 
is inside the line segment PQ on r or not.

Algorithm.

n = u x (Q - P)
SP = P - S
SQ = Q - S
proj_SP = SP - ( (n . SP) / (n . n) )  n 
proj_SQ = SQ - ( (n . SQ) / (n . n) )  n
w = n x u
if (proj_SP . w) * (proj_SQ . w) < 0
    then the point on r that is closest to line s 
         is inside the line segment PQ
else
         the point on r that is closest to line s 
         is outside the line segment PQ