JavaScript array DFS but always back to root after searching-CodePudding

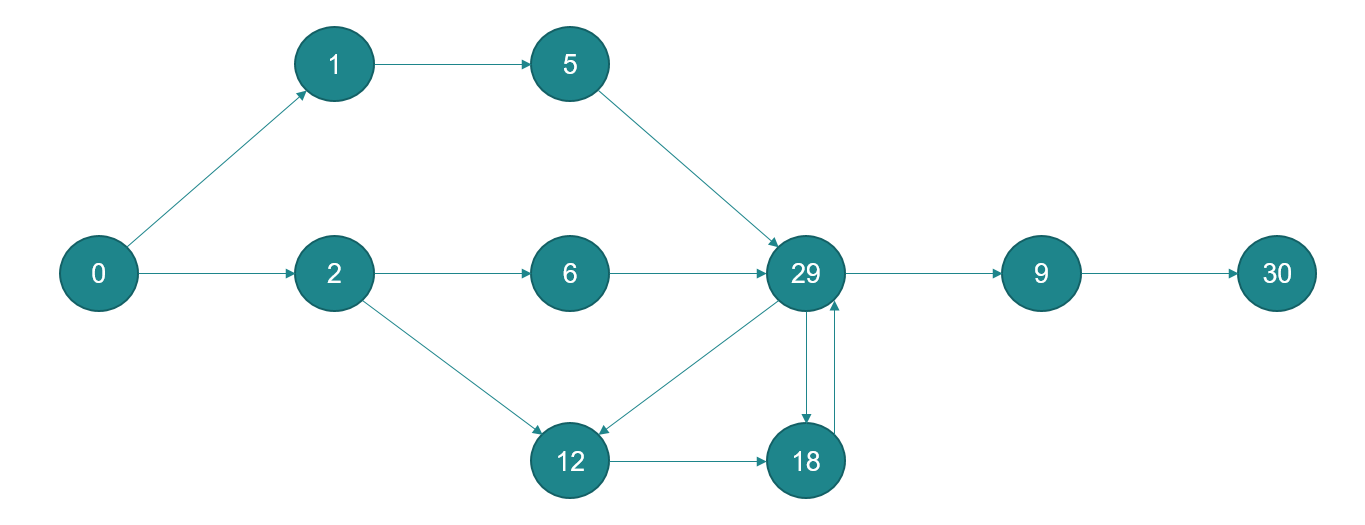
I'd like to get output from input.
It should be passed all the ways that is possible but shouldn't be passed the way which was already visited.
It looks similar with Depth-First Search but this should be returned to parent node and then search again.
The logic is the last element of one node should be the same with the first element of another node.
And it should start with 0 and finish when there is no more node for searching.

input = [  
  [0, 1],
  [0, 2],
  [1, 5],
  [2, 6],
  [2, 12],
  [5, 29],
  [6, 29],
  [9, 30],
  [12, 18],
  [18, 29],
  [29, 9],
  [29, 12],
  [29, 18]
];

output =  [
  [0,1,5,29,9,30],
  [0,1,5,29,12,18,29,18],
  [0,1,5,29,12,18,29,9,30],
  [0,1,5,29,18,29,9,30],
  [0,1,5,29,18,29,12,18],
  [0,2,6,29,9,30],
  [0,2,6,29,12,18,29,9,30],
  [0,2,6,29,12,18,29,18],
  [0,2,6,29,18,29,9,30],
  [0,2,6,29,18,29,12,18],
  [0,2,12,18,29,9,30],
  [0,2,12,18,29,12],
  [0,2,12,18,29,18]
]

I tried recursion like below and it showed undefined. Setting for visited object seems making undefined, but it showed maximum call stack if I edited it.
(It doesn't matter either recursive or iterative ways to solve this problem.)

Please please help. Any comment would be helpful.

const seeds = input.filter( ele => ele[0] === 0);
const nodes = input.filter( ele => ele[0] !== 0);
const visited = {};

function chain(seed, nodes){
  let result = nodes.map(node => {
    if(node[0] === seed[seed.length - 1]){
      while(!visited[node]){
        visited[node]= true;
        return chain([...seed, node[0]], nodes)
      }
    }
  })
  return result;
}

function getResult(seeds, nodes){
  let result = seeds.map( seed => {
  visited[seed] = true;
    return chain(seed, nodes);
  }).flat();
  return result;
}

CodePudding user response：

I assume your graph is a directed graph, and a "way" will use one particular edge only once.

I would suggest building an adjacency list first. One that is keyed by vertices, and for each of them has an array of edges (not neighboring vertices alone).

Then in the DFS you can collect the edges that you visit as you go deeper in the tree, and then test that a new edge can only be added to that list when it does not yet occur in that chain yet. This is the major difference with the "normal" DFS procedure, where you would collect vertices (instead of edges) as you build a path.

Here is the implementation with a generator:

function* dfs(adj, vertex=0, path=[]) {
    let leaf = true;
    for (let edge of adj[vertex]) {
        if (!path.includes(edge)) {
             yield* dfs(adj, edge[1], path.concat([edge]));
             leaf = false;
        }
    }
    if (leaf) yield path.map(edge => edge[0]).concat(vertex);
}

const input = [[0, 1], [0, 2], [1, 5], [2, 6], [2, 12], [5, 29], [6, 29], [9, 30], [12, 18], [18, 29], [29, 9], [29, 12], [29, 18]];

// Build adjacency list as key/value pairs, where key=vertex, 
//    and value=array of outgoing edges (not just the neighbors)
const adj = {};
for (let edge of input) {
    (adj[edge[0]] ??= []).push(edge);
    adj[edge[1]] ??= [];
}

// Output paths
for (let path of dfs(adj)) console.log(JSON.stringify(path));

The input graph is your graph:

The output is:

[0,1,5,29,9,30]
[0,1,5,29,12,18,29,9,30]
[0,1,5,29,12,18,29,18]
[0,1,5,29,18,29,9,30]
[0,1,5,29,18,29,12,18]
[0,2,6,29,9,30]
[0,2,6,29,12,18,29,9,30]
[0,2,6,29,12,18,29,18]
[0,2,6,29,18,29,9,30]
[0,2,6,29,18,29,12,18]
[0,2,12,18,29,9,30]
[0,2,12,18,29,12]
[0,2,12,18,29,18]