Simulate a strange distribution in R-CodePudding

Hi all I'm attempting to simulate data that looks something like this: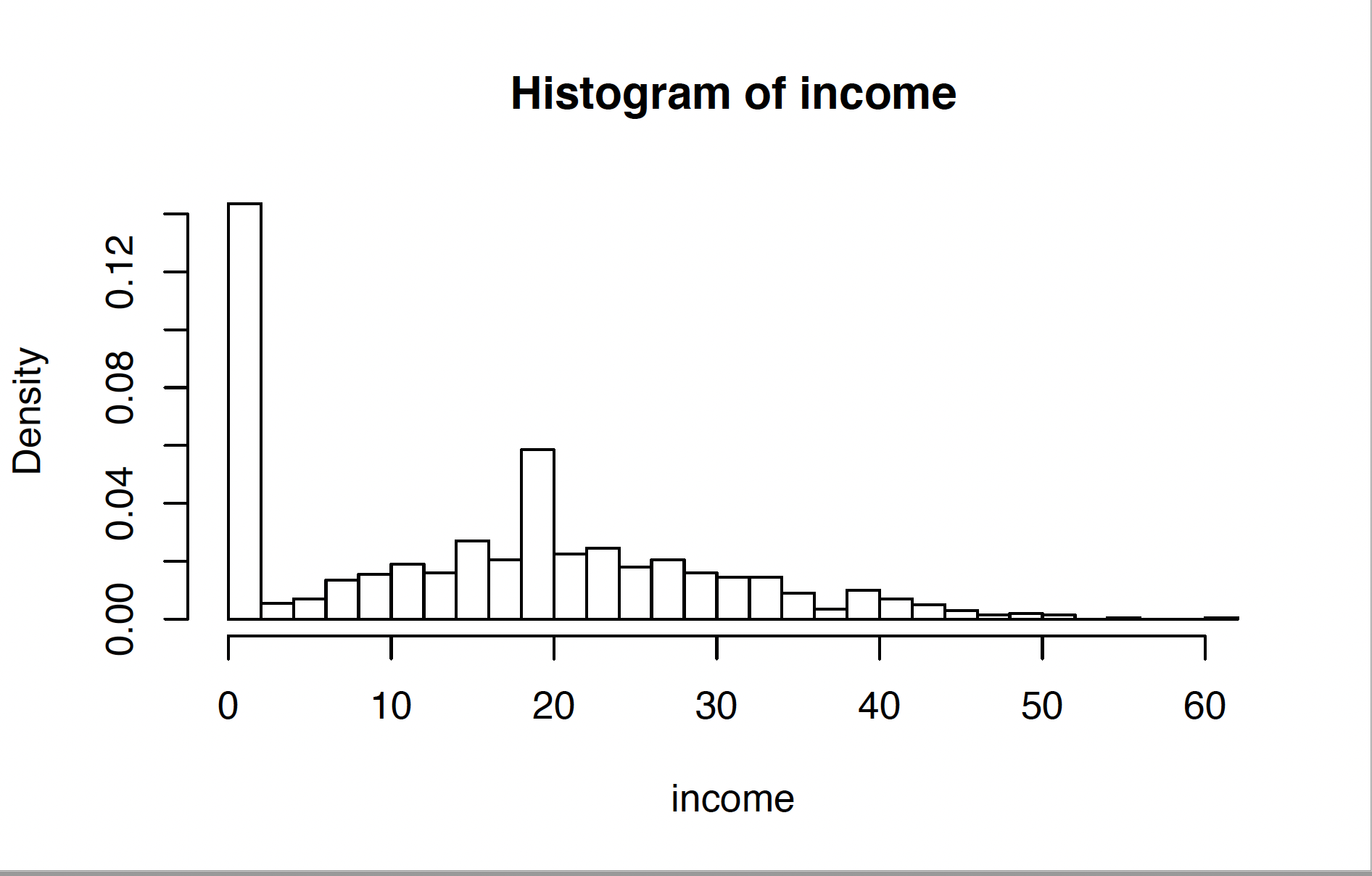

Anyone know how I'd go about doing this?

CodePudding user response：

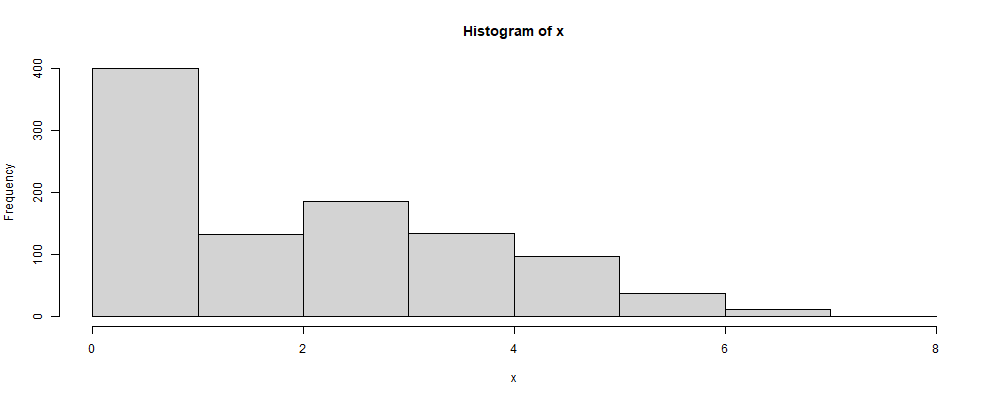
This can be considered as a classical problem to transform uniform random numbers generated with runif with an inverse transformation from empirical relative frequencies. Here an approach that uses approx:

freq <- c(0.39, 0.02, 0.15, 0.18, 0.12, 0.09,0.04, 0.01)
sum(freq) # This is a check. The sum must be 1.0.

r_empirical <- function(n, freq) {
  approx(c(0, cumsum(freq)), 0:(length(freq)),
         runif(n), method="constant", f=0)$y
}

x <- r_empirical(1000, freq)

hist(x, breaks=0:length(freq))

generated distrigbution

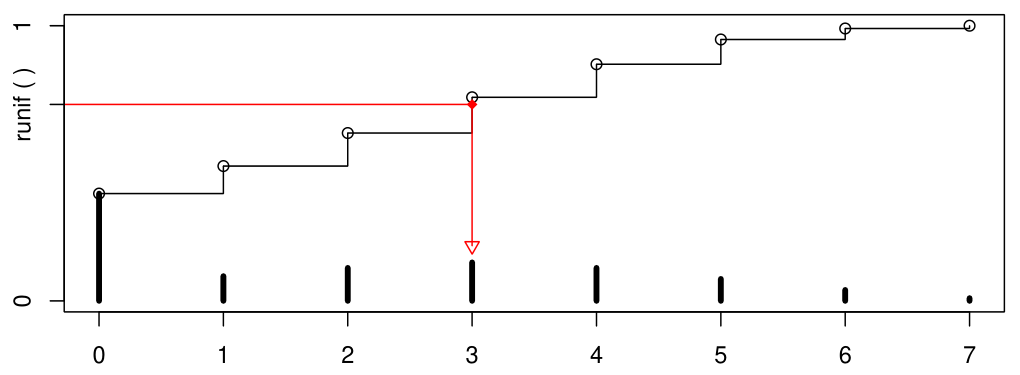
The following figure demonstrates the basic principle. The stairs show the cumulative distribution, the red arrows how a uniform random number can be transformed:

inverse transform

CodePudding user response：

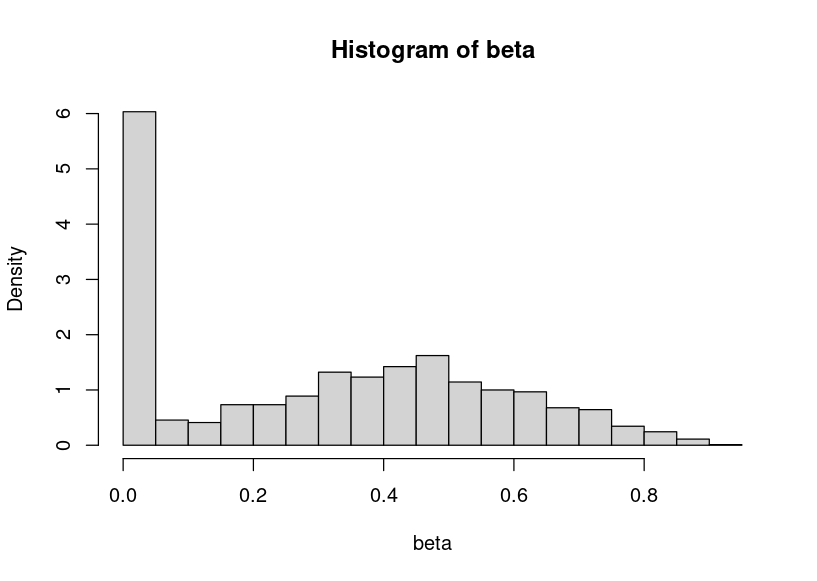
you could also use two beta distributions.

Beta is a very useful distribution.

beta<-c(rbeta(600, 0.1, 5, ncp = 0),rbeta(1200, 3, 4, ncp = 1))

hist(beta,breaks=30,probability = T)

CodePudding user response：

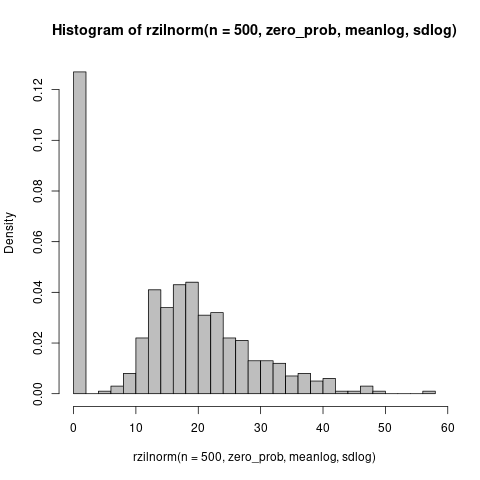
Zero-inflated log-Normal? (Spike at zero looks a little too big for a Tobit, i.e. censored Normal with the negative stuff piled up on zero)

zero_prob <- 0.25
meanlog <- log(20)
sdlog <- 0.4 ## SD ~ 40%

n <- 500
rzilnorm <- function(n, pz, meanlog, sdlog) {
   ifelse(runif(n) < pz, 0,
          rlnorm(n, meanlog, sdlog))
}
set.seed(101)
hist(rzilnorm(n=500, zero_prob, meanlog, sdlog), col = "gray", breaks=25, freq=FALSE)

My first try was with n=100 and pz=0.2; if I were going to play around with this more I might increase sdlog a little bit. Otherwise this looks pretty close?