Computing profile confidence intervals for a regression line-CodePudding

Simulate some data

n       <- 50
beta0   <- 2
beta1   <- 0.32
x       <- runif(n=n, min=0, max=5)
mu      <- exp(beta0   beta1 * x)
y       <- rpois(n=n, lambda=mu)
data    <- data.frame(x=x, y=y)
plot(data$x, data$y)

Apply a Poisson regression

glm.pois <- glm(formula= y ~ x, data=data, family=poisson(link="log"))
summary(glm.pois)

Compute profile 95% CI

(pCI <- confint(glm.pois))
nice.xs <- sort(data$x)
pred.pCI   <- apply(t(pCI), 1, FUN=function(x){exp( x[1] x[2]*nice.xs)})

Compute 95% CI using the SE

new.dat <- data.frame(phat = predict(glm.pois, type="response"),
                      x  = data$x)
new.dat <- new.dat[with(new.dat, order(x)), ]
ilink <- poisson()$linkinv

## Add fit and se.fit on the link scale
new.dat <- bind_cols(new.dat, 
     setNames(as_tibble(predict(glm.pois, new.dat, 
                           se.fit = TRUE)[1:2]), 
              c('fit_link','se_link')))
new.dat <- mutate(new.dat,
                  fit  = ilink(fit_link),
                  right_upr = ilink(fit_link   (2 * se_link)),
                  right_lwr = ilink(fit_link - (2 * se_link)))

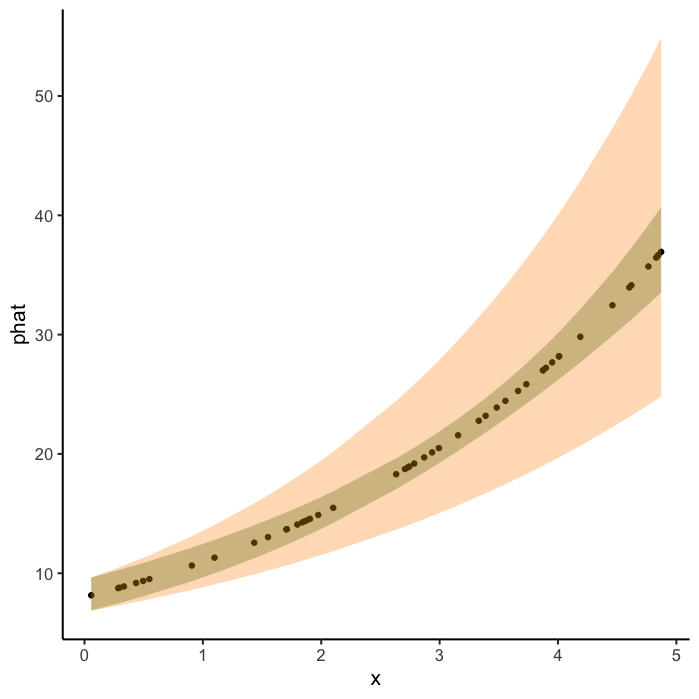
Plot

ggplot(data=new.dat, aes(x=x, y= phat))   
    geom_point()   
    geom_ribbon(aes(x=x, ymin =right_lwr, ymax = right_upr), 
                fill = "darkgreen", alpha=0.3)  
    geom_ribbon(aes(x=nice.xs, ymin = pred.pCI[,1], ymax = pred.pCI[,2]), 
                fill = "darkorange", alpha=0.3)  
    theme_classic(base_size=15)

My question is why are the profile 95% CI (orange ribbon) so large? I imagine I am computing them wrong but I don't know where my mistake is.

CodePudding user response：

There is a very strong correlation between the intercept and slope:

cov2cor(vcov(glm.pois))
            (Intercept)          x
(Intercept)   1.0000000 -0.9147526
x            -0.9147526  1.0000000

Your profile CIs, which are computing (logistic(intercept_lwr slope_lwr*x) and logistic(intercept_upr slope_upr*x), are ignoring this correlation.

It's not easy to compute profile confidence intervals on derived values (i.e., on quantities other than the parameters themselves).