Use bootstrapping to estimate 95% confidence interval for slope coefficient-CodePudding

I have this code below:

set.seed(1)
n <- 100
x <- rnorm(n)
y <- 5   3*x   rnorm(n, mean = 0, sd = 0.3)
df <- data.frame(x=x,y=y)
slope <- lm(y~x, data = df)$coefficients[2]

I want to use 100 bootstrap samples to estimate a 95% confidence interval for the slope coefficient. I've never done bootstrapping before so I'm a little stuck. I know I want to use sample to sample 100 indices from 1:n with replacement. I also know I need the standard error of the slope to calculate CI. However, when I do stderr<- sd(slope)/sqrt(length(slope)) I get <NA>. Just not sure how to translate that into R. I should get the CIs to be (2.95, 3.05).

CodePudding user response：

A single bootstrap sample of c(1, 2, 3, 4, 5) can be sampled via sample(c(1, 2, 3, 4, 5), 5, TRUE). Many can be drawn using replicate on that:

# this was your original code
set.seed(1)
n <- 100
x <- rnorm(n)
y <- 5   3*x   rnorm(n, mean = 0, sd = 0.3)
df <- data.frame(x=x,y=y)

# before we do many bootstrap samples, first define what happens in each one of them    
one_regr <- function(){
  mysample <- sample(1:n, n, TRUE) # which observations pairs are in this 
                                   # bootstrap sample?
  my_df <- df[mysample, ]
  slope <- lm(y  ~x, data = my_df)$coefficients[2]
  return(slope)
}

# test run -- works!
one_regr()

# now we can do many replicates with replicate()
many_slopes <- replicate(5000, one_regr())
hist(many_slopes, breaks = 30)
quantile(many_slopes, c(.025, .975))

Addition 1:

You can have more fun with this if you sample not only the slopes but the intercepts as well as in

one_regr <- function(){
  mysample <- sample(1:n, n, TRUE) # which observation pairs are in this 
                                   # bootstrap sample?
  my_df <- df[mysample, ]
  return( lm(y  ~x, data = my_df)$coefficients )
}

many_lines <- replicate(5000, one_regr())
intercepts <- many_lines[1,]
slopes <- many_lines[2,]
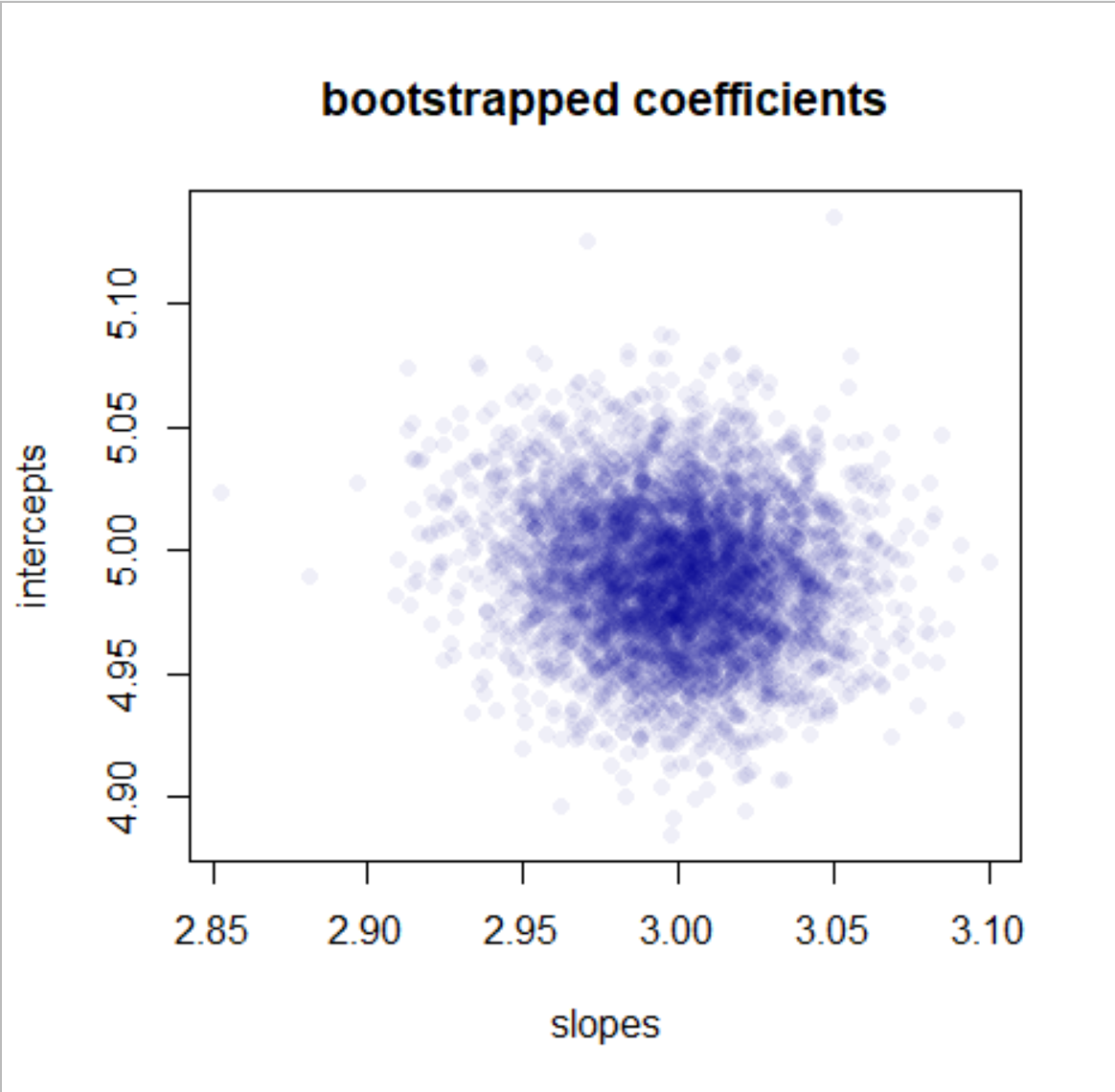
plot(df$x, df$y, main = "data and 500 regression lines")
for(i in 1:5000){   # just draw the regression lines
    abline(a = intercepts[i], b = slopes[i], col = "#00009001")
}
plot(slopes, intercepts, main = "bootstrapped coefficients", 
     pch = 16, col = "#00009010")
quantile(slopes, c(.025, .975))

Addition 2:

https://www.investopedia.com/terms/s/standard-error.asp states:

The standard error (SE) of a statistic is the approximate standard deviation of a statistical sample population.

So the standard error of the slope is the standard deviation of our bootstrapped slopes:

> sd(slopes)
[1] 0.02781162

roughly, this should be 4 times the width of the 95%-CI:

> sd(slopes)
[1] 0.02781162
> abs(2.95 - 3.05)/4
[1] 0.025