is there any way to check if a line output of LSD is vertical or horizontal-CodePudding

I am using LSD: LineSegmentDetector in python and OpenCV, now the problem is I want to count num of horizontal lines detected and number of vertical lines detected.

img = cv2.imread("test/images.jpg")
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
thresh = cv2.threshold(gray, 100, 200, cv2.THRESH_BINARY_INV   cv2.THRESH_OTSU)[1]
linesL = lsd(gray)
for line in linesL:
    x1, y1, x2, y2, width = map(int,line)
    length = line_length(x1,y1,x2,y2)
    if line[-1]<3:
        lines_img = cv2.line(img, (x1,y1), (x2,y2), (0,0,0),1)
show_img(lines_img,"FLD")

Output

Lines Array [[x1,y1,x2,y2,width],....]

I have tried morphological operations and houghlinesP as well but they aren't performing well.

CodePudding user response：

As you know the coordinates of the endpoints, you could simply compute the slope of the line with

slope = (y2 - y1) / (x2 - x1)

If the slope is 0, then the line is horizontal, if it's infinity, then the line is vertical. In practice, you'll rarely have slopes equal to 0 or infinity. So simply put a threshold like:

if abs(slope) < 1:
    print("It's an horizontal line!")
elif abs(slope) > 100:
    print("It's a vertical line!")
else:
    print("It's... a line!")

One other simple solution, if you really care only for horizontal and vertical lines, is to compare x values, and y values:

if abs(x1 - x2) < 5:
    print("It's a vertical line!")
elif abs(y1 - y2) < 5:
    print("It's an horizontal line!")
else:
    print("It's... a line!")

Edit: I added the absolute value to the slope comparisons.

CodePudding user response：

We can use slope for this problem. We know the the slope of a line in angles would be the arctan of the ration of difference of ys and xs

slope_as_angle = atan((y1 - y2) / (x1 - x2))

It's a good practice to use atan2 instead of atan. and for simplicity let's use degrees instead of radians:

slope_as_angle = math.degrees(math.atan2((y1 - y2), (x1 - x2)))

Now let's see how lines would look like for different slope angles:

for i in range(0, 360, 20):
    x = 10 * math.cos(math.radians(i))
    y = 10 * math.sin(math.radians(i))
    spl = math.degrees(math.atan2(y - 0, x - 0)) % 360

    plt.plot([0, x], [0, y], label=str(i))

plt.legend()
plt.show()

Please notice we are getting slope angles for all lines between (0, 0) and (cos, sin) (See: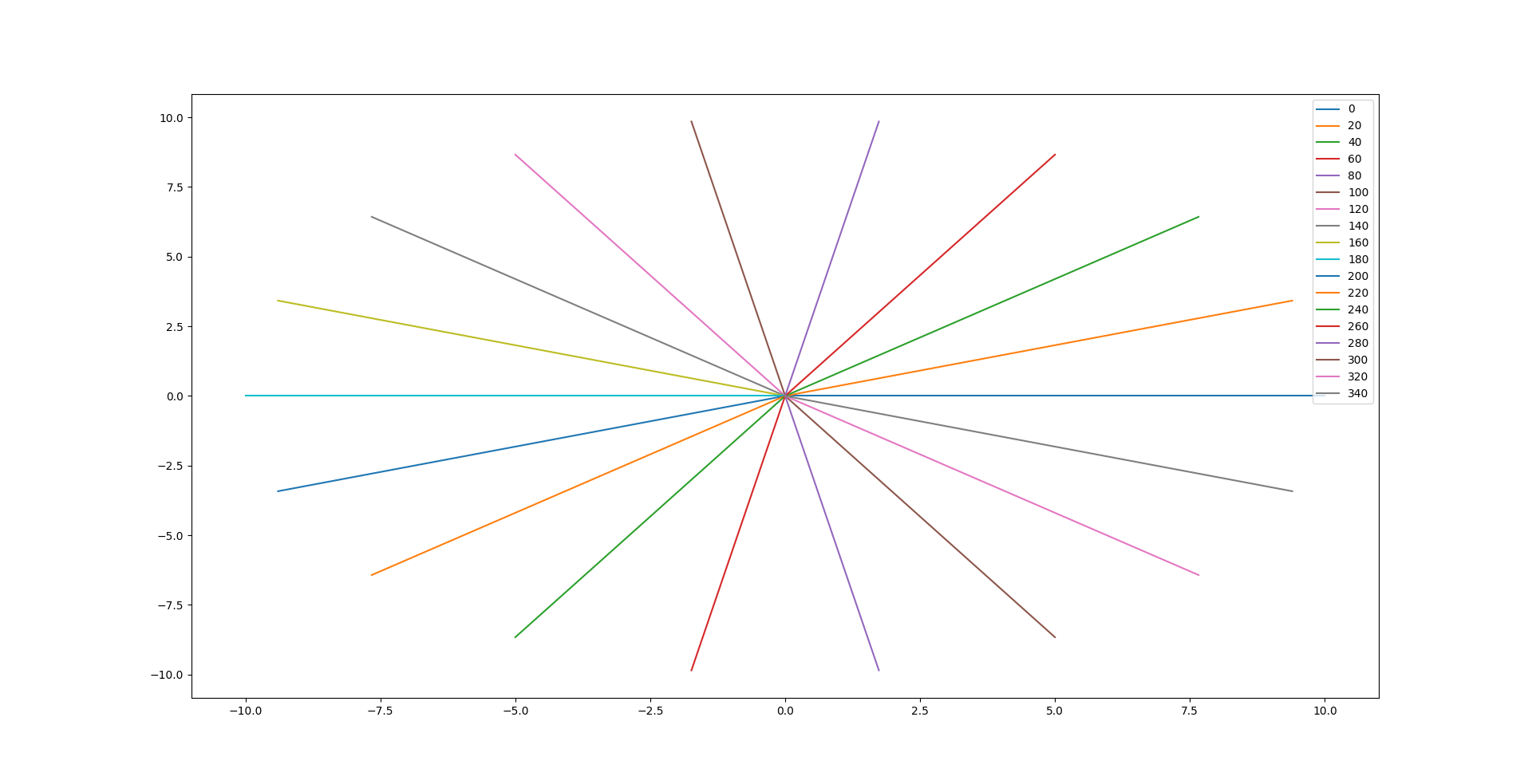

Now we need a logic to understand if a line is vertical or horizontal by given slope angle:

Horizontal

I would say each line with slope angles between [160, 200] or bigger then 340 or smaller then 20 is horizontal.

if 160 < angle < 200 or 340 < angle or angle < 20

Better way:

if 160 < angle < 200 or not 20 < angle < 340

Vertical

I would say each line with slope angles between [60, 120] or [240, 300] is vertical.

if 60< angle < 120 or 240 < angle < 300.

Let's assign a limit variable as a threshold so we can change it as will:

for horizontal lines:

if (not limit < spl <= 360 - limit) or (180 - limit <= spl < 180   limit):

for vertical lines:

if (90 - limit < spl < 90   limit) or (270 - limit < spl < 270   limit):

The code to check would be:

def check_the_line(slope, limit=10):
    if (not limit < spl <= 360 - limit) or (180 - limit <= spl < 180   limit):
        return "h"
    elif (90 - limit < spl < 90   limit) or (270 - limit < spl < 270   limit):
        return "v"
    
    return "o"

Let's validate:

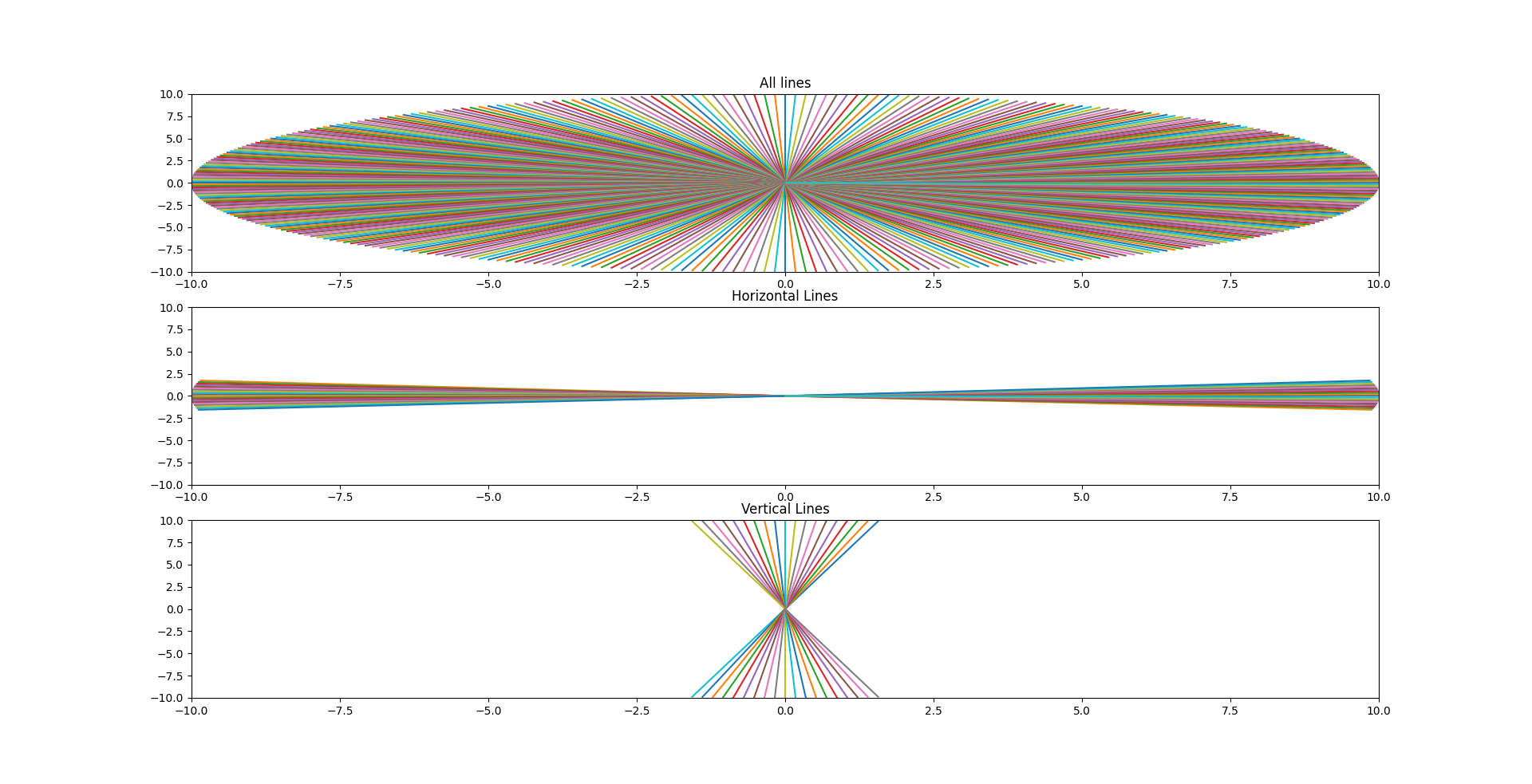
import math
from matplotlib import pyplot as plt

fig, (ax1, ax2, ax3) = plt.subplots(3, 1)

limit = 10


def check_the_line(slope, limit=10):
    if (not limit < spl <= 360 - limit) or (180 - limit <= spl < 180   limit):
        return "h"
    elif (90 - limit < spl < 90   limit) or (270 - limit < spl < 270   limit):
        return "v"

    return "o"


for i in range(0, 360, 1):
    x = 10 * math.cos(math.radians(i))
    y = 10 * math.sin(math.radians(i))
    spl = math.degrees(math.atan2(y, x)) % 360

    ax1.plot([0, x], [0, y])
    if check_the_line(spl, limit=limit) == "h":
        ax2.plot([0, x], [0, y])
    elif check_the_line(spl, limit=limit) == "v":
        ax3.plot([0, x], [0, y])

ax1.set_title("All lines")
ax1.set_xlim([-10, 10])
ax1.set_ylim([-10, 10])

ax2.set_title("Horizontal Lines")
ax2.set_xlim([-10, 10])
ax2.set_ylim([-10, 10])

ax3.set_title("Vertical Lines")
ax3.set_xlim([-10, 10])
ax3.set_ylim([-10, 10])
plt.show()