How to get a smooth continuous pdf of a Bayesian Gaussian mixture model?-CodePudding

Given the code below

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

from sklearn.mixture import BayesianGaussianMixture

df = pd.read_csv("dataset", delimiter=" ")
data = df.to_numpy()
X_train = np.reshape(data, (10*data.shape[0],2))

bgmm = BayesianGaussianMixture(n_components=15,
                               random_state=7,
                               max_iter=5000,
                               n_init=10,
                               weight_concentration_prior_type="dirichlet_distribution")

bgmm.fit(X_train)
logprob = bgmm.score_samples(X_train)
pdf = np.exp(logprob)

x = np.linspace(0, 1, num=20)
plt.plot(x, pdf, '-k', label='Mixture PDF')
plt.show()

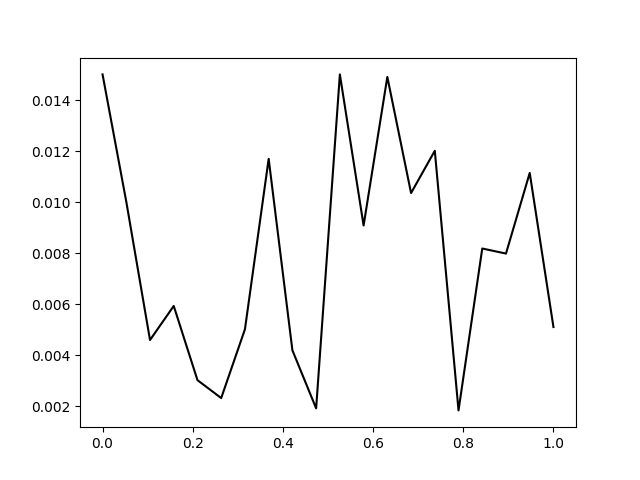
I get the following discrete pdf:

How can I plot a smooth continuous version of this pdf?

Edit:

Here is the the dataset:

[[6.11507621 6.2285484 ]
 [5.61154419 7.4166868 ]
 [5.3638034  8.64581576]
 [8.58030274 6.01384676]
 [2.06883754 8.5662325 ]
 [7.772149   2.29177372]
 [0.66223423 0.01642353]
 [7.42461573 5.46288677]
 [0.82355307 3.60322705]
 [1.12966405 9.54888118]
 [4.34716189 3.63203485]
 [7.95368286 5.74659859]
 [3.21564946 3.67576324]
 [6.48021187 7.35190659]
 [3.02668358 4.41981514]
 [0.01745485 7.49153586]
 [1.08490595 0.91004064]
 [1.89995405 0.38728879]
 [4.40549506 2.48715052]
 [4.52857064 1.24935027]]

CodePudding user response：

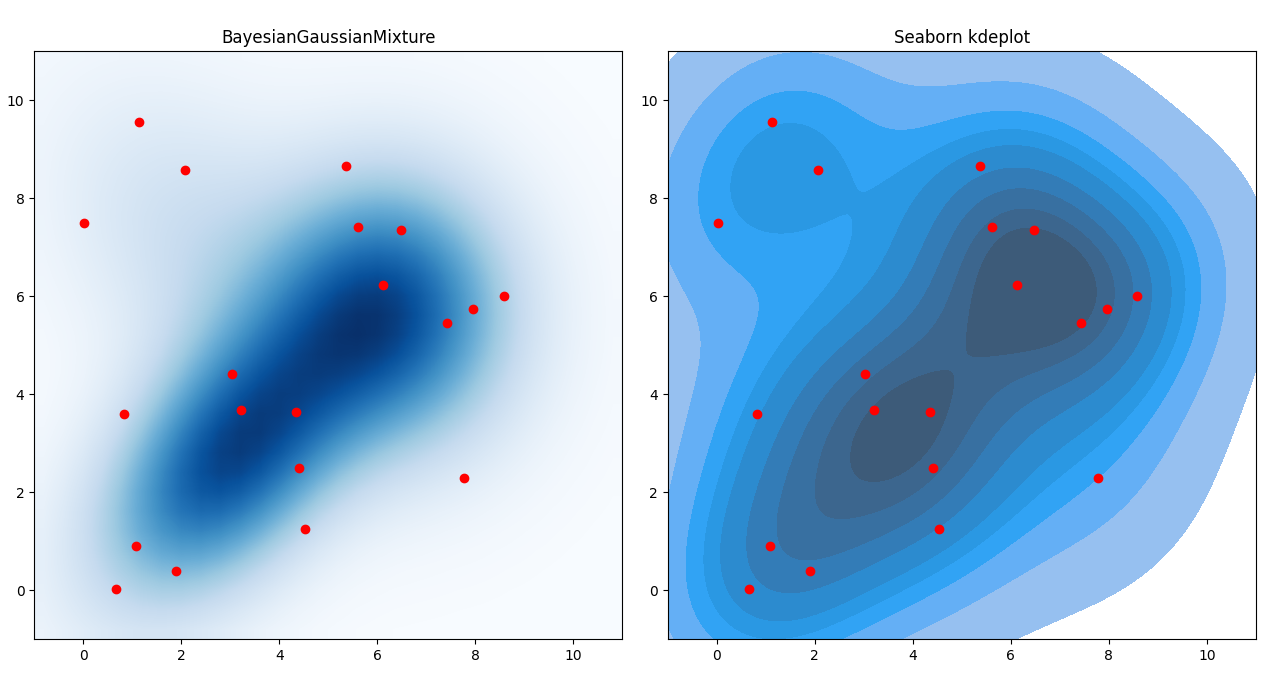
If the data are x and y values in 2D, you could try the following code to start experimenting:

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.mixture import BayesianGaussianMixture

data = np.array([[6.11507621, 6.2285484], [5.61154419, 7.4166868], [5.3638034, 8.64581576], [8.58030274, 6.01384676],
                 [2.06883754, 8.5662325], [7.772149, 2.29177372], [0.66223423, 0.01642353], [7.42461573, 5.46288677],
                 [0.82355307, 3.60322705], [1.12966405, 9.54888118], [4.34716189, 3.63203485], [7.95368286, 5.74659859],
                 [3.21564946, 3.67576324], [6.48021187, 7.35190659], [3.02668358, 4.41981514], [0.01745485, 7.49153586],
                 [1.08490595, 0.91004064], [1.89995405, 0.38728879], [4.40549506, 2.48715052], [4.52857064, 1.24935027]])


X_train = data

bgmm = BayesianGaussianMixture(n_components=15,
                               random_state=7,
                               max_iter=5000,
                               n_init=10,
                               weight_concentration_prior_type="dirichlet_distribution")

bgmm.fit(X_train)
# create a mesh of points with x and y values going from -1 to 11
x, y = np.meshgrid(np.linspace(-1, 11, 30), np.linspace(-1, 11, 30))
# recombine x and y to tuples
xy = np.array([x.ravel(), y.ravel()]).T
logprob = bgmm.score_samples(xy)
pdf = np.exp(logprob).reshape(x.shape)

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))

# show the result of bgmm.score_samples on a mesh
ax1.imshow(pdf, extent=[-1, 11, -1, 11], cmap='Blues', interpolation='bilinear', origin='lower')
# show original data in red
ax1.scatter(data[:, 0], data[:, 1], color='red')
ax1.set_title('BayesianGaussianMixture')

# create a seaborn kdeplot from the same data
sns.kdeplot(x=data[:, 0], y=data[:, 1], fill=True, ax=ax2)
ax2.scatter(data[:, 0], data[:, 1], color='red')
ax2.set_aspect('equal', 'box')
ax2.set_xlim(-1, 11)
ax2.set_ylim(-1, 11)
ax2.set_title('Seaborn kdeplot')

plt.tight_layout()
plt.show()