Trouble plotting a rotated right triangle in matplotlib-CodePudding

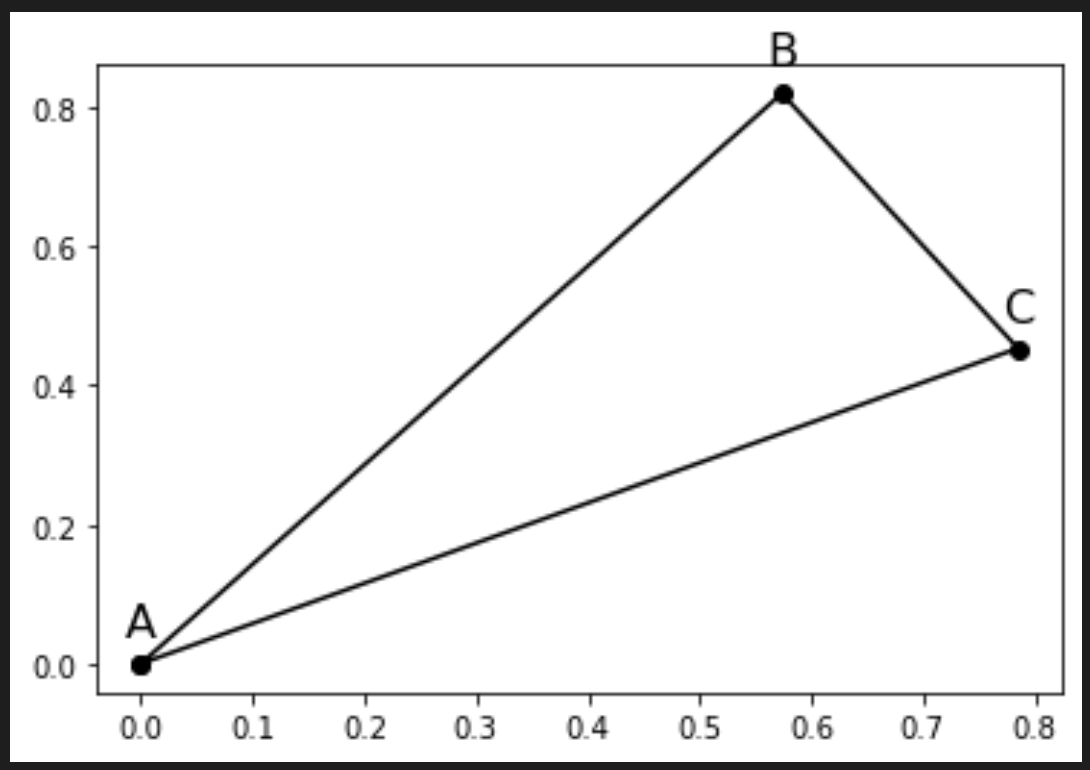
I'm trying to generate a right triangle with hypotenuse = 1, interior angle 25, that is rotated 30 degrees. I've entered the trig formulas correctly to my understanding, and I suspect some kind of rounding error. Because the triangle produced in matplot is slightly off from a right triangle.

import math
import matplotlib.pyplot as plt
from annotation import label

angle_b = math.radians(25) # the interior 25 degree angle of our right triangle
angle_a = math.radians(30) # 30 degree angle between the plotted angle_b triangle and the x axis.

point_A = (0,0)
point_B = (math.cos(angle_a   angle_b), math.sin(angle_a   angle_b))
point_C = (math.cos(angle_a) * math.cos(angle_b), math.sin(angle_a) * math.cos(angle_b))

# Label our points
label(plt, 'A', point_A)
label(plt, 'B', point_B)
label(plt, 'C', point_C)

# Draw the right triangle between our points.
plt.plot(*zip(point_A, point_B, point_C, point_A), marker='o', color='black')

As you can see, the angle ACB is not a right angle as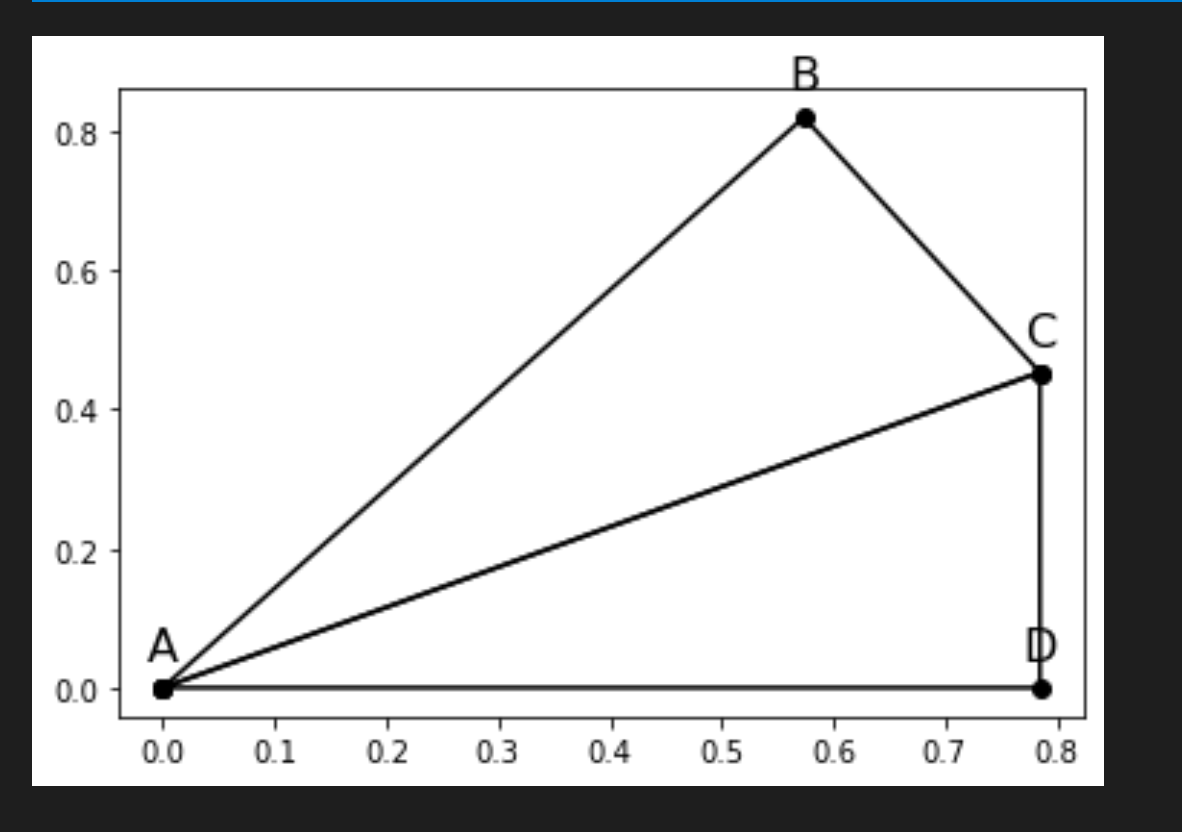

CodePudding user response：

You appear to have jumbled your trigonometry. I'm going to suggest moving slowly step-by-step, and using variable names that help you remember what is going on.

Let's start with the original triangle. If interior_angle = np.deg2rad(25) and the hypotenuse has length 1, then the right angle on the x-axis is at (np.cos(interior_angle), 0) and the other interior angle is at (np.cos(interior_angle), np.sin(interior_angle)). Neither of the points in your diagram corresponds.

Now let's express the triangle as a matrix whose columns are the vertices:

interior_angle = np.deg2rad(25)
vertices = np.array([
    [0, np.cos(interior_angle), np.cos(interior_angle), 0],
    [0, 0, np.sin(interior_angle), 0],
])

The last vertex is a repeat of the origin to make plotting easier.

Now let's look at the rotation. For rotation_angle = np.deg2rad(30), point (x, y) rotates to (np.cos(rotation_angle) * x - np.sin(rotation_angle) * y, np.sin(rotation_angle) * x np.cos(rotation_angle) * y). This can be expressed as a matrix equation:

rotation_matrix = np.array([
    [np.cos(rotation_angle), -np.sin(rotation_angle)],
    [np.sin(rotation_angle), np.cos(rotation_angle)]])
p_out = rotation_matrix @ p_in

The array vertices is so constructed that it can be directly multiplied by a rotation matrix. You can therefore write

rotation_angle = np.deg2rad(30)
rotation_matrix = np.array([
    [np.cos(rotation_angle), -np.sin(rotation_angle)],
    [np.sin(rotation_angle), np.cos(rotation_angle)]])
rotated_vertices = rotation_matrix @ vertices

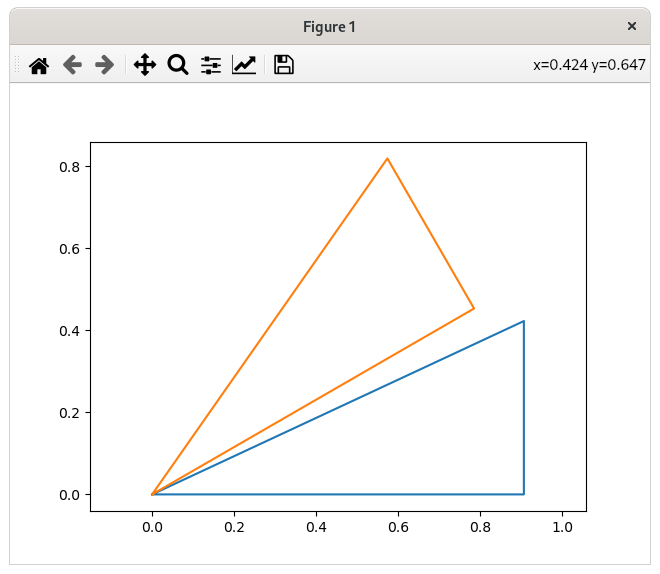
The plotted image should make more sense now:

plt.plot(*vertices)
plt.plot(*rotated_vertices)
plt.axis('equal')
plt.show()

CodePudding user response：

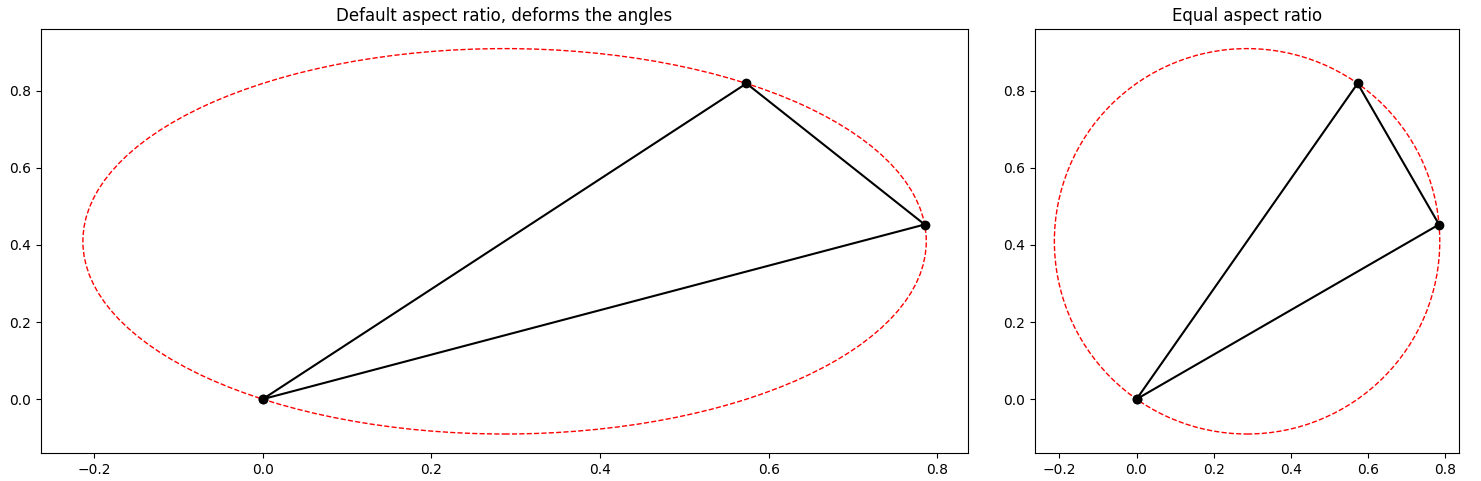
The problem is that by default, matplotlib doesn't use the same distances in the x and in the y direction. Instead, matplotlib tries to fit everything nicely into the given bounds.

These uneven distances distort angles, and also deforms circles.

You can force an equal aspect ratio via ax.set_aspect('equal').

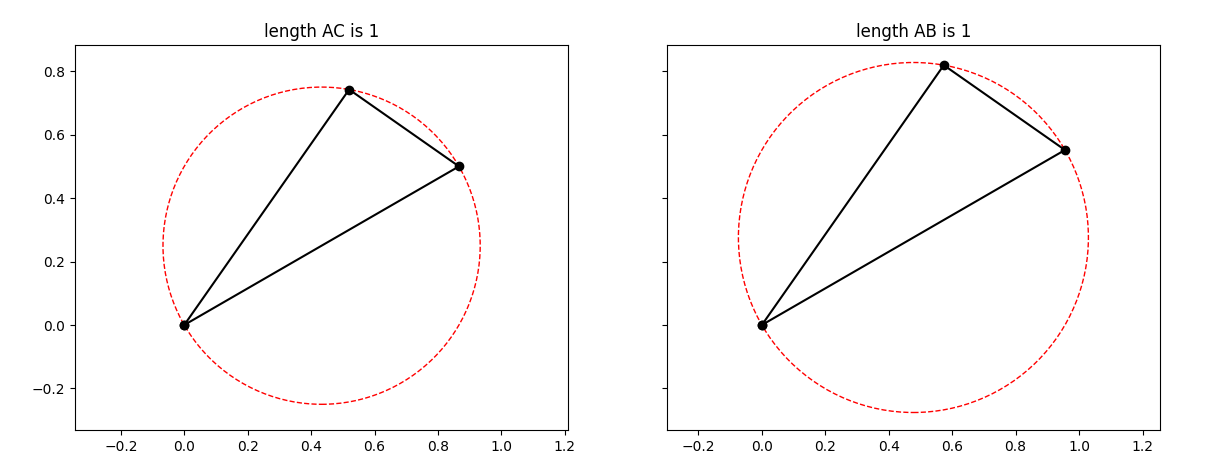
To calculate the positions via the angles, and have the right corner at point B, you need to take into account that the length AC is cos(b) times the length of AC. AC can be chosen to have 1 as length. Alternatively, you could divide both B and C by cos(b) to have a larger triangle, where the length of AB would be 1.

import matplotlib.pyplot as plt
import math

angle_b = math.radians(25)  # the interior 25 degree angle of our right triangle
angle_a = math.radians(30)  # 30 degree angle between the plotted angle_b triangle and the x axis.

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(14, 5), sharey=True)

for ax in (ax1, ax2):
    point_A = (0, 0)
    if ax == ax1:
        point_B = (math.cos(angle_a   angle_b) * math.cos(angle_b), math.sin(angle_a   angle_b) * math.cos(angle_b))
        point_C = (math.cos(angle_a), math.sin(angle_a))
        ax.set_title('length AC is 1')
    else:
        point_B = (math.cos(angle_a   angle_b), math.sin(angle_a   angle_b))
        point_C = (math.cos(angle_a) / math.cos(angle_b), math.sin(angle_a) / math.cos(angle_b))
        ax.set_title('length AB is 1')
    point_M = ((point_A[0]   point_C[0]) / 2, (point_A[1]   point_C[1]) / 2)

    # Draw the right triangle between our points.
    ax.plot(*zip(point_A, point_B, point_C, point_A), marker='o', color='black')
    # draw a circle around the 3 points
    ax.add_patch(plt.Circle(point_M, math.sqrt((point_M[0] - point_A[0]) ** 2   (point_M[1] - point_A[1]) ** 2),
                            ec='r', ls='--', fc='none'))
    ax.set_aspect('equal', 'datalim')

plt.show()

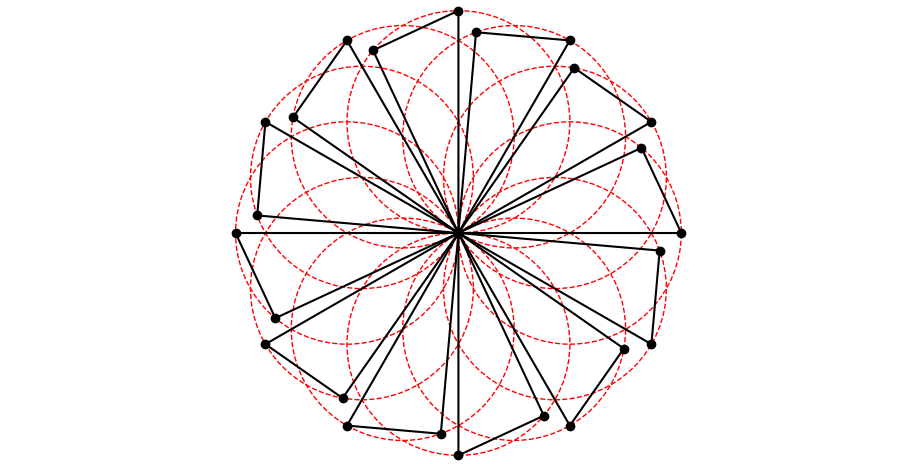
The same calculation works for any angle. Here is how 12 rotations in steps of 30 degrees look together:

The following code shows the effect of ax.set_aspect('equal') for the original points.

import matplotlib.pyplot as plt
import math

angle_b = math.radians(25)  # the interior 25 degree angle of our right triangle
angle_a = math.radians(30)  # 30 degree angle between the plotted angle_b triangle and the x axis.

point_A = (0, 0)
point_B = (math.cos(angle_a   angle_b), math.sin(angle_a   angle_b))
point_C = (math.cos(angle_a) * math.cos(angle_b), math.sin(angle_a) * math.cos(angle_b))

point_M = ((point_A[0]   point_B[0]) / 2, (point_A[1]   point_B[1]) / 2)

fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(16, 4), gridspec_kw={'width_ratios': [2, 1]})

for ax in (ax1, ax2):
    # Draw the right triangle between our points.
    ax.plot(*zip(point_A, point_B, point_C, point_A), marker='o', color='black')
    # draw a circle around the 3 points
    ax.add_patch(plt.Circle(point_M, math.sqrt((point_M[0] - point_A[0]) ** 2   (point_M[1] - point_A[1]) ** 2),
                            ec='r', ls='--', fc='none'))
ax1.set_title('Default aspect ratio, deforms the angles')
ax2.set_aspect('equal')  # or plt.axis('equal')
ax2.set_title('Equal aspect ratio')
plt.tight_layout()
plt.show()