Rotation torus in matplotlib3d-CodePudding

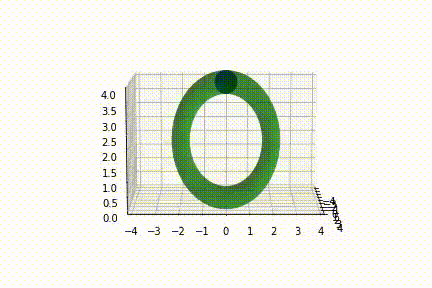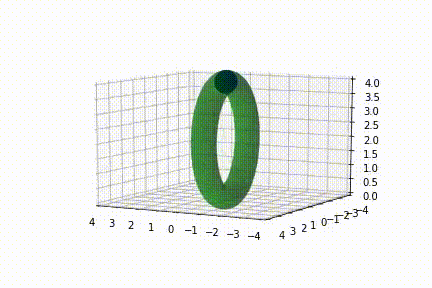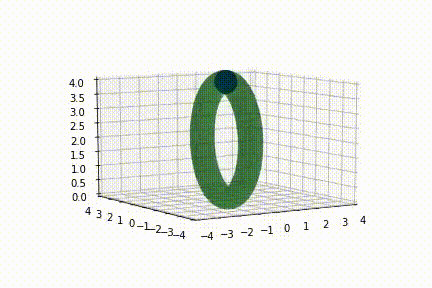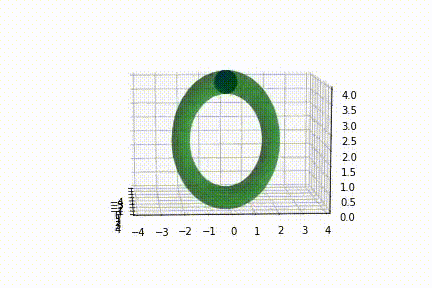
Recently I started working with matplotlib. Can you help how I can rotate(spin) animation a torus around Oz? I tried to change the values of x,y,z in the update function, but this changes the location of the torus, not its rotation.

import matplotlib.pyplot as plt
import matplotlib.animation as animation

t = np.linspace(0, 2 * np.pi, 50)
th, ph = np.meshgrid(t, t)
r = 0.4
x, y, z = 1.5*r * np.sin(ph), (2   r * np.cos(ph)) * np.sin(th), (2   r * np.cos(ph)) * np.cos(th)
Steps = 1001
fig = plt.figure()

ax = fig.add_subplot(projection='3d')
plot=[ax.plot_surface(x, y, z 2,rstride=2,cstride=1,color='green',alpha=.5)]

ax.set(xlim=[-4, 4], ylim=[-4, 4], zlim=[0, 4])
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)

a = 0.5 * np.outer(np.cos(u), np.sin(v))
b = 0.5 * np.outer(np.sin(u), np.sin(v))
c = 0.4 * np.outer(np.ones(np.size(u)), np.cos(v))
elev = 10.0
rot = 80.0 / 180 * np.pi
ax.plot_surface(a, b, c 4,  rstride=4, cstride=4, color='b', linewidth=0)
theta = np.linspace(0, 20 * np.pi,1001)
ax.view_init(elev = elev, azim = 0)
def update(num):
    plot[0].remove()
    x, y, z = 1.5 * r * np.sin(ph), (2   r * np.cos(ph)) * np.sin(th), (2   r * np.cos(ph)) * np.cos(th)
    plot[0] = ax.plot_surface(1.5 * r * np.sin(ph),(2   r*np.cos(ph)) * np.sin(th),(z 2),rstride=2,cstride=1,color='green',alpha=.5)
ani = animation.FuncAnimation(fig, update, 100,interval=40)
ax.elev = 60
plt.show() ```

CodePudding user response：

One way to do this is to just change the value of the azim argument of the ax.view_init function in your update function. You can for instance add the line ax.view_init(azim=360*num/100, elev=10). That way, the point of view rotates around the z-axis at every frame. See full code below:

import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np

t = np.linspace(0, 2 * np.pi, 50)
th, ph = np.meshgrid(t, t)
r = 0.4
x, y, z = 1.5*r * np.sin(ph), (2   r * np.cos(ph)) * np.sin(th), (2   r * np.cos(ph)) * np.cos(th)
Steps = 1001
fig = plt.figure()

ax = fig.add_subplot(projection='3d')
plot=[ax.plot_surface(x, y, z 2,rstride=2,cstride=1,color='green',alpha=.5)]

ax.set(xlim=[-4, 4], ylim=[-4, 4], zlim=[0, 4])
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)

a = 0.5 * np.outer(np.cos(u), np.sin(v))
b = 0.5 * np.outer(np.sin(u), np.sin(v))
c = 0.4 * np.outer(np.ones(np.size(u)), np.cos(v))
elev = 10.0
rot = 80.0 / 180 * np.pi
ax.plot_surface(a, b, c 4,  rstride=4, cstride=4, color='b', linewidth=0)
theta = np.linspace(0, 20 * np.pi,1001)
ax.view_init(elev = elev, azim = 0)
def update(num):
    plot[0].remove()
    x, y, z = 1.5 * r * np.sin(ph), (2   r * np.cos(ph)) * np.sin(th), (2   r * np.cos(ph)) * np.cos(th)
    plot[0] = ax.plot_surface(1.5 * r * np.sin(ph),(2   r*np.cos(ph)) * np.sin(th),(z 2),rstride=2,cstride=1,color='green',alpha=.5)
    ax.view_init(azim=360*num/100, elev=10)
ani = animation.FuncAnimation(fig, update, 100,interval=40)
plt.show()

And this is what the output looks like at 30fps: