Plotting a 95% confidence interval band around a predicted regression line from a linear mixed model-CodePudding

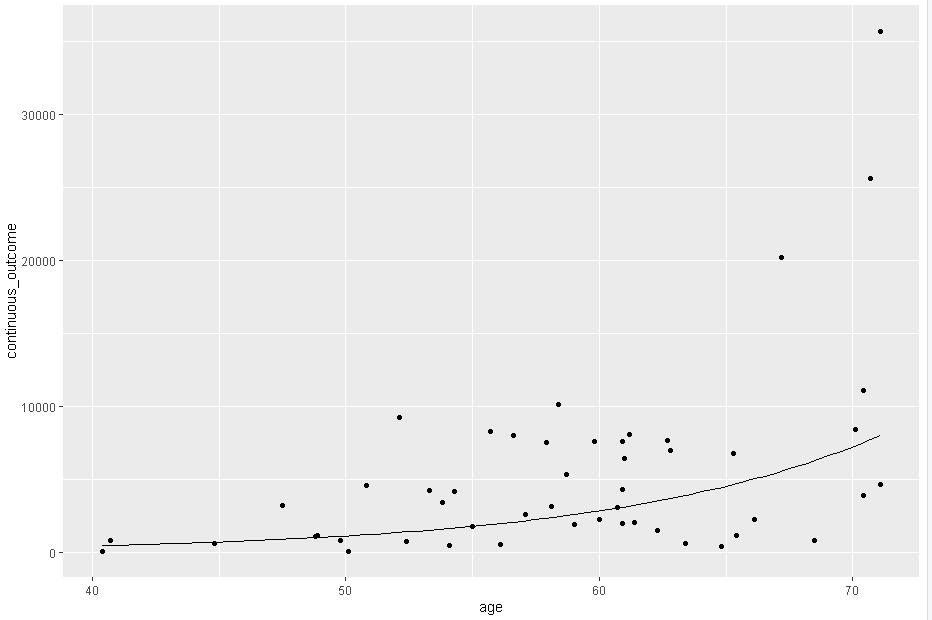
To make the results that I obtained from a linear mixed model more insightful, I'm trying to plot the predicted values with a 95% confidence interval.

The data and the model that I specified look as follows:

library(ggplot2)
library(magrittr)
library(nlme)

mydata <- structure(list(pat_id = c(61, 8, 179, 13, 153, 80, 273, 142, 
202, 2, 61, 127, 135, 49, 20, 25, 315, 48, 157, 171, 29, 271, 
105, 14, 14, 84, 180, 125, 255, 135, 39, 49, 320, 160, 197, 189, 
154, 77, 30, 75, 50, 103, 115, 80, 88, 34, 310, 81, 75, 82), 
    age = c(57.1, 61.4, 60.9, 58.7, 65.4, 44.8, 59, 47.5, 63.4, 
    59.8, 55, 66.1, 50.8, 62.8, 71.1, 48.9, 58.1, 49.8, 71.1, 
    56.6, 50.1, 40.4, 62.3, 53.3, 53.8, 70.4, 67.2, 68.5, 57.9, 
    54.3, 60.9, 61, 54.1, 70.1, 52.4, 70.4, 55.7, 60.7, 56.1, 
    60.9, 60, 52.1, 48.8, 40.7, 58.4, 65.3, 62.7, 64.8, 61.2, 
    70.7), continuous_outcome = c(2605.440900389, 2063.9, 1929.46472167969, 
    5341.496223986, 1119.6044921885, 566.255950927734, 1880.5290222168, 
    3215.77453613281, 603.7692803513, 7594.527875667, 1775.66680908203, 
    2260.04156843471, 4565.098635412, 6948.76321012, 35685.6, 
    1170.96138000488, 3152.85720825195, 765.9703779527, 4638.270794249, 
    7962.890625, 45.4402923583984, 76.2939453125, 1466.9, 4207.615392583, 
    3410.15625, 11076.9451141357, 20190.12993463, 822.127334531, 
    7512.78955078125, 4146.38368225098, 4292.35992431641, 6393.09959411621, 
    465.39306640625, 8409, 737.1825748757, 3898.624597663, 8238.67454528809, 
    3054.98580932617, 526.4287617193, 7612.90808598633, 2247.54676818848, 
    9231.37016296387, 1067.416015625, 775.980377197266, 10118.2, 
    6744.3, 7616.49208068848, 356.531524658203, 8069.160616877, 
    25596.8906372702), continuous_outcome_log = c(7.86574093001633, 
    7.63283707807243, 7.56551604134912, 8.58344828040522, 7.0216235438582, 
    6.34081061444271, 7.53984003495667, 8.07613443965171, 6.40484703050537, 
    8.93531491566494, 7.48249430865052, 7.72358085708673, 8.42641442900534, 
    8.84646286749209, 10.4825305471662, 7.06643401737976, 8.05638149327426, 
    6.64244817996005, 8.44231247645808, 8.98267293141324, 3.83816745221036, 
    4.34761562539111, 7.29158808696319, 8.34488898720956, 8.13480658905054, 
    9.31271148408861, 9.9129986748043, 6.71311090867393, 8.92449521812674, 
    8.33023297640332, 8.36482490452301, 8.76313090568181, 6.14502876872992, 
    9.03717675296699, 6.60419118543475, 8.26863557047525, 9.01671612519243, 
    8.02485750673053, 6.26801380735694, 8.93773186515778, 7.71803940572248, 
    9.13047108358574, 6.97393247141267, 6.65541509547637, 9.22218988833333, 
    8.81660124504343, 8.93820247123851, 5.87922353910847, 8.99592866402467, 
    10.1502652300912), fu_time = c(2.19, 4.005, 0, 0.857, 0.745, 
    4.153, 1.522, 0, 0.12, 3.184, 0, 0.802, 0.517, 1.859, 0.268, 
    0, 0, 0.799, 0.446, 0.78, 0, 0, 2.185, 0.953, 1.457, 3.888, 
    0.268, 1.295, 0, 3.967, 4.375, 0, 0, 0.479, 0.159, 1.29, 
    0, 0, 0.734, 0, 0, 0, 3.584, 0, 0.997, 1.106, 1.506, 0, 0.307, 
    0)), row.names = c(NA, -50L), class = c("tbl_df", "tbl", 
"data.frame"))

regression <- 
  lme(fixed=continuous_outcome_log ~ 1   fu_time   age*fu_time,
      random=~1|pat_id, 
      data=mydata, 
      correlation=corCAR1(form=~1   fu_time|pat_id),
      na.action="na.omit",
      method="REML", 
      control=lmeControl(opt="optim"))

To plot the predicted values I've first created a prediction dataframe (pframe) as follows:

pframe <- 
  expand.grid(
    fu_time=mean(mydata$fu_time),
    age=seq(min(mydata$age), max(mydata$age), length.out=75))

pframe$predicted_continuous_outcome <- 
  exp(predict(regression, newdata=pframe, level=0))

Next, I've plotted the predicted values over the observed values as follows:

predict_plot <- 
  mydata %>% 
  ggplot(
    data=., 
    aes(x=age, y=continuous_outcome))   
  geom_point()  
  geom_line(
    data=pframe, 
    aes(x=age, y=predicted_continuous_outcome))
predict_plot

How do I predict and plot a 95% confidence interval around the predictions in pframe? I tried pframe$ci <- exp(predict(regression, newdata=pframe, interval="confidence")) but that produces an error: Error in predict.lme(regression, newdata = pframe, interval = "confidence") : cannot evaluate groups for desired levels on 'newdata'

CodePudding user response：

There doesn't appear to be a predict method for lme that can do confidence intervals. But they can be calculated manually (following calculations here). Possibly a good job for a function to predict your three values of interest:

library(ggplot2)
library(magrittr)
library(nlme)
library(dplyr)

pframe <- 
  expand.grid(
    fu_time=mean(mydata$fu_time),
    age=seq(min(mydata$age), max(mydata$age), length.out=75))

constructCIRibbon <- function(newdata, model) {

  df <- newdata %>%
    mutate(Predict = predict(model, newdata = ., level = 0))
  
  mm <- model.matrix(eval(eval(model$call$fixed)[-2]), data = df)
  
  vars <- mm %*% vcov(model) %*% t(mm)
  sds <- sqrt(diag(vars))
  
  df %>% mutate(
    lowCI = Predict - 1.96 * sds,
    HiCI = Predict   1.96 * sds,
    across(Predict:HiCI, exp)
  )
}

pframe <- constructCIRibbon(pframe, regression)

mydata %>% 
  ggplot(aes(age, continuous_outcome))  
  geom_point()  
  geom_line(data = pframe, aes(y = Predict))  
  geom_ribbon(data = pframe,
              aes(y = Predict, ymin = lowCI, ymax = HiCI), 
              alpha = 0.2)

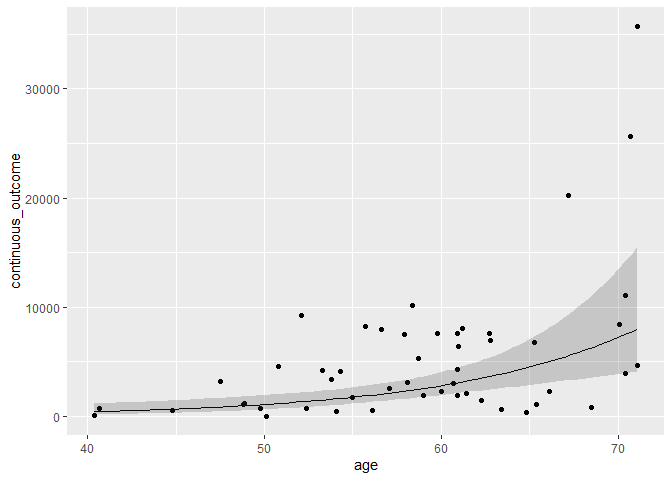
^{Created on 2021-12-15 by the reprex package (v2.0.1)}