Dijkstra shortest path on multiple unweighted graphs?-CodePudding

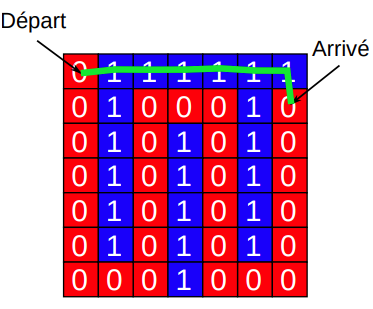
I'm trying to figure out how to implement djiktra algorithm to find the shortest path between 2 unweighted graphs. The suggestion I got was to use 2 graphs one for the red color and one for the blue color.The cost is always 1 to travel but to access a red square while being blue you need to pay 2 to switch graph.

I'm mostly looking for suggestions and references has anyone done something similar ???

CodePudding user response：

Create a new weighted graph based on the original graph where a blue -> red path costs 3 instead of 1, then run Dijkstra on that.

Edit: it's probably not necessary to actually create the new graph, you can get the weights directly from the original graph, but creating the new graph first is probably easier to follow at first.

The top corner would look like this:

A ← 3 → B ← 1 → C ← 1 → D ...
↑       ↑       ↑
1       1       3  
↓       ↓       ↓
E ← 3 → F ← 3 → G...

CodePudding user response：

This is simply standard Dijkstra.

This is not an unweighted graph, you have a cost of moving from one vertex to another. There is just an extra rule in the swapping from one color to another bares an additional cost.

All you need is a function to calculate the cost between two vertexes that simply looks at the color of each vertex and increases the cost appropriately. See: int getCost(Graph const& graph, Point src, Point dst) below.

Other than that it is a standard algorithym you should be applying.

// Not pure C  
// But left enough work that you have to make an effort
// to complete this.

enum Color { Red, Blue};
using Graph = std::vector_like<std::vector_like<Color>>;
using Point = std::pair<int, int>;

int getCost(Graph const& graph, Point src, Point dst)
{
    // Assumes: src and dst are 1 point away from each other.
    //          This assumes that work is done via
    //          getListOfPointsReachable() which only gets nodes
    //          nodes that are adjecent.
    //          
    // Standard movement cost.
    int cost = 1;

    // Add a cost if switching between blue red.
    if (graph[src] !=  graph[dst]) {
        cost  = 2;
    }
    return cost;
}

std::list<Point> getListOfPointsReachable(Graph const& graph, Point src)
{
    // Get a list of points that can be accessed by src.
    // All points that are next to the current and return as a list.
    // Check if they are out of bounds.
}

void Dijkstra(Graph const& graph, Point start, Point end)
{
    std::set<Point>  visited;

    // Boundary:  int   => Cost
    //            Point => Point cost applies to.
    // Using tuple as it already has the comparison operator defined.
    using Boundary = std::tuple<int, Point>;
    std:: priority_queue<Boundary>   boundary;

    // Set up the boundary list with a start.
    boundary.emplace(0, start);

    while (!boundary.empty())
    {
        Boundary next = boundry.top();
        boundary.pop();

        int      cost = std::get<0>(next);
        Point    nextP = std::get<1>(next);

        if (nextP == end)
        {
            throw std::runtime_error("Found route to end: Cheapest Route is: "   cost);
        }
        if (visited.find(nextP) != std::end(visited))
        {
            // we already did this node.
            continue;
        }
        visited.insert(nextP);

        std::list<Point> dests = getListOfPointsReachable(graph, nextP);
        for (auto const& dest: dests)
        {
            int extraCost = getCost(graph, nextP, dest);
            boundary.emplace(extraCost   cost, dest);
        }
    }
    throw std::runtime_error("No Route from Start to End");
 }

CodePudding user response：

To create the graph, use this psuedo code to add edges between nodes

AddEdge( n1, n2 )
SET cost = 1
IF n1color != n2color
   SET cost = 3;
graph.AddEdge( n1, n2, cost );
RUN Dijsktra on graph