I am aiming for a sequential neural network with two neurons capabale of reproducing a quadratic function. To do this, I chose the activation function of the first neuron to be lambda x: x**2, and the second neuron to be None.

Each neuron outputs A(ax b) where A is the activation function, a is the weight for the given neuron, b is the bias term. Output of the first neuron is passed onto the second neuron, and the output of that neuron is the result.

The form of the output of my network is then:

Training the model means to adjust the weights and biases of each neuron. Choosing a very simple set of parameters, ie:

leads us to a parabola which should be perfectly learnable by a 2-neuron neural net descibed above:

To implement the neural network, I do:

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

Define function to be learned:

f = lambda x: x**2   2*x   2

Generate training inputs and outputs using above function:

np.random.seed(42)
questions = np.random.rand(999)
solutions = f(questions)

Define neural network architecture:

model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=1, input_shape=[1],activation=lambda x: x**2),
  tf.keras.layers.Dense(units=1, input_shape=[1],activation=None)
])

Compile net:

model.compile(loss='mean_squared_error',
              optimizer=tf.keras.optimizers.Adam(0.1))

Train the model:

history = model.fit(questions, solutions, epochs=999, batch_size = 1, verbose=1)

Generate predictions of f(x) using the newly trained model:

np.random.seed(43)
test_questions = np.random.rand(100)
test_solutions = f(test_questions)

test_answers = model.predict(test_questions)

Visualize result:

plt.figure(figsize=(10,6))
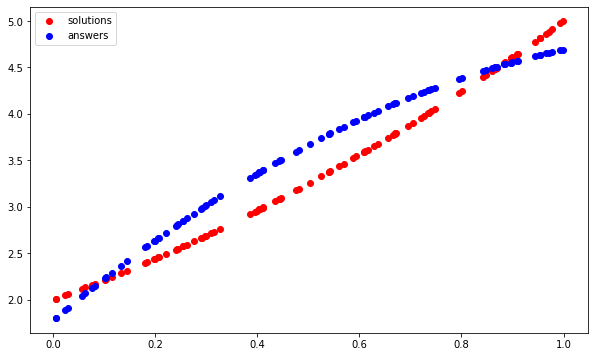
plt.scatter(test_questions, test_solutions, c='r', label='solutions')
plt.scatter(test_questions, test_answers, c='b', label='answers')
plt.legend()

The red dots form the curve of the parabola our model was supposed to learn, the blue dots form the curve which it has learnt. This approach clearly did not work.

What is wrong with the approach above and how to make the neural net actually learn the parabola?

CodePudding user response：

Fix using proposed architecture

Decreasing a learning rate to 0.001 does the trick, compile like this instead:

model.compile(loss='mean_squared_error',
              optimizer=tf.keras.optimizers.Adam(0.001))

Visualize new results:

plt.figure(figsize=(10,6))
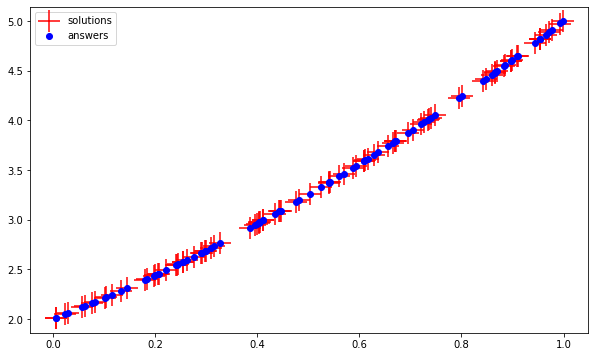
plt.scatter(test_questions, test_solutions, c='r',marker=' ', s=500, label='solutions')
plt.scatter(test_questions, test_answers, c='b', marker='o', label='answers')
plt.legend()

Nice fit. To check the actual weights to know what parabola exactly was learnt, we can do:

[np.array(layer.weights) for layer in model.layers]

Output:

[array([-1.3284513, -1.328055 ], dtype=float32),
 array([0.5667597, 1.0003909], dtype=float32)]

Expected 1, 1, 1, 1, but plug these values back to the equation

Coefficient of x^2 term:

0.5667597*(-1.3284513)**2 # result: 1.0002078022990382

Coefficient of x term:

2*0.5667597*-1.3284513*-1.328055 # result: 1.9998188460235597

Constants terms:

0.5667597*(-1.328055)**2 1.0003909 # result: 2.000002032736224

Ie the learnt parabola is:

1.0002078022990382 * x**2   1.9998188460235597 * x   2.000002032736224

Which is pretty close to f, ie x**2 2*x 2.

Reassuringly, the difference between the coefficients of the learned parabola and the true parabola is less than the learning rate.

Note that we can use an even simpler architecture

ie:

model = tf.keras.Sequential([
  tf.keras.layers.Dense(units=1, input_shape=[1],activation=lambda x: x**2),
])

Ie we have a neuron with output (a*x b)**2, and through training a & b are adjusted -> we can describe any parabola like this as well. (Did actually try this too, it worked.)

CodePudding user response：

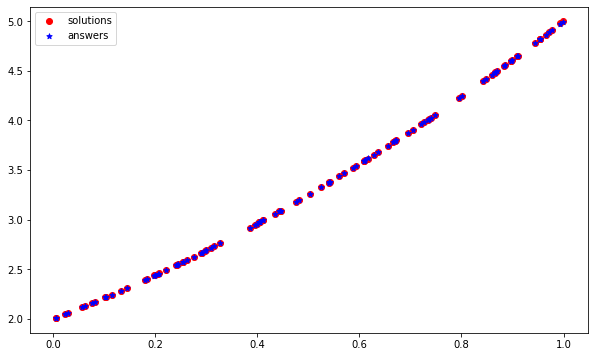
To add to @Zabob's answer. You have used Adam optimizer which is sensitive to the initial learning rate, and while it is considered quite robust, I have found that it is sensitive to the initial learning rate- and can result in unexpected results (as in your case where it is learning opposite curve). If you change the optimizer to SGD:

model.compile(loss='mean_squared_error',
              optimizer=tf.keras.optimizers.SGD(0.01))

Then in less than 100 epochs, you can get an optimized network: