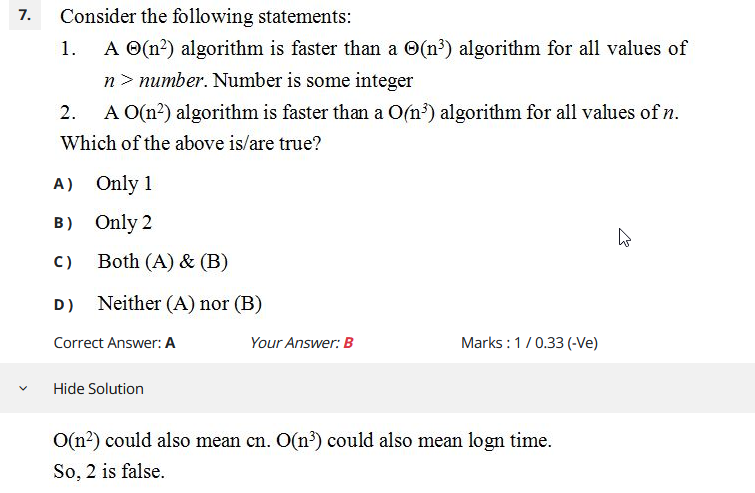
I have a doubt in this particular question where the answer says that big-Oh(n^2) algorithm will not run faster than big-Oh(n^3) algorithm whereas if the notation in both cases was theta instead then it would have been true but why is that so?

I would love it if anyone could explain it to me in detail because I couldn't find any source from where my doubt could get clarified.

CodePudding user response：

Part 1 paraphrased (note the phrasing in the question is ambiguous where "number" is quantified -- it has to be picked after you choose the two algorithms, but I assume that's what's intended).

Given functions f and g with f=Theta(n^2) and g=Theta(n^3), then there exists a number N such that f(n) < g(n) for all n>N.

Part 2 paraphrased:

Given functions f and g with f=O(n^2) and g=O(n^3), then for all n, f(n) < g(n).

1 is true, and you can prove it by application of the definition of big-Theta.

2 is false (as a general statement), and you can disprove it by finding a single example of f and g for which it is false. For example, f(n) = 2, g(n) = 1. Big O is a kind of upper bound, so these constant functions work. The counter-examples given in the question are f(n)=n, g(n)=log(n), but the same principle applies.

CodePudding user response：

the answer says that big-Oh(n^2) algorithm will not run faster than big-Oh(n^3) algorithm

It is more subtle: an O(